Question

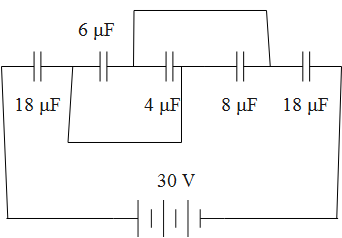
Five capacitors are connected to each other as shown. What is the potential drop and charge across the $4\mu F$ capacitor?

$A.\,6V,30\mu C$
$B.\,10V,30\mu C$
$C.\,6V,40\mu C$
$D.\,10V,40\mu C$

Answer 1

Firstly, we will compute the equivalent capacitance of the capacitors of the given circuit. Then, we will compute the potential drop across the capacitor $4\mu F$. And, then, the charge on the capacitor is calculated using the potential drop obtained.

Formula used:

& {{C}_{P}}={{C}_{1}}+{{C}_{2}}+... \\\ & {{V}_{S}}=\dfrac{V}{n} \\\ & C=\dfrac{Q}{V} \\\ \end{aligned}$$ **Complete step by step answer:** Consider the given circuit diagram while going through the following steps. From the figure, it’s clear that the capacitors 6, 4 and 8 are parallel to each other. Thus, we will compute the parallel capacitance. The formula for calculating the parallel capacitance is as follows. $${{C}_{P}}={{C}_{1}}+{{C}_{2}}+...$$ Substitute the values of the capacitance of the capacitors in the above equation. $$\begin{aligned} & {{C}_{648}}=6+4+8 \\\ & \Rightarrow {{C}_{648}}=18\mu F \\\ \end{aligned}$$ Now, the capacitors, 18, 18 and 18 have the same capacitance value and even are parallel to each other. Thus, the potential drop across each capacitor is calculated as follows. The formula for calculating the voltage across the series capacitors with the same capacitance value. $${{V}_{S}}=\dfrac{V}{n}$$ Where V is the potential drop value and n is the number of series capacitors having the same capacitance value. Substitute the values in the above equation. $$\begin{aligned} & {{V}_{S}}=\dfrac{30}{3} \\\ & \Rightarrow {{V}_{S}}=10\,V \\\ \end{aligned}$$ Now let us compute the charge on the capacitor $$4\mu F$$. We know that the potential drop across the parallel capacitors is equal, thus, the voltage drop across the $$4\mu F$$ capacitor will be the same as the 10 V. Therefore, the charge on the capacitor $$4\mu F$$ is, $$\begin{aligned} & Q=CV \\\ & \Rightarrow Q=4\mu \times 10 \\\ & \therefore Q=40\mu C \\\ \end{aligned}$$ Therefore, the potential drop and the charge across the capacitor $$4\mu F$$ is, 10 V and As the value of the potential drop and charge across the $$4\mu F$$ capacitor is 10 V and $$40\mu C$$, **Thus, the option (D) is correct.** **Note:** This question is a direct one, except, if we know how to find the capacitance of the capacitors arranged in a circuit as given. The units of the parameters should be taken care of while solving these types of problems like nano, micro, etc.