Question
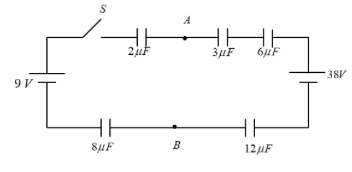
Question: Five capacitors are connected as shown in the figure. Initially \(S\) is opened and all the capacito...
Five capacitors are connected as shown in the figure. Initially S is opened and all the capacitors are uncharged. When S is closed and steady state is obtained, then find out the potential difference between the points A and B .
Solution
To calculate the potential difference between the points A and B we first need to calculate the net capacitance in the circuit, then find the net voltage in the circuit. Using this we find the net charge in the circuit which helps us to find the potential drops at points A and B. Finally, we apply Kirchhoff’s Voltage Law to get the final answer.
Complete step by step solution:
We see in the diagram that the circuit has five capacitors in series. So, we first calculate the net capacitance in the circuit.
The capacitors are in series so we use the formula of series combination of capacitances which is equal to calculating resistors in parallel combination.
C1=C11+C21+C31+C41+C51
⇒C1=2μX1+3μF1+6μX1+12μF1+8μF1
⇒C1=24μF29
⇒C=2924μF
Thus, the net capacitance in the circuit is C=2924μF
Now, we calculate the net voltage in the circuit.
We can see that there are two voltages which are connected opposite to each other, so to calculate the net potential we find the difference between the two potentials.
⇒Vnet=V1−V2
⇒Vnet=38V−9V
⇒Vnet=29V
Thus, the net voltage in the circuit is Vnet=29V
Now that we know the net capacitance and net voltage in the circuit, we can find the total charge in the circuit using the formula Q=CV where Q is the net charge.
⇒Q=2924μF×29V
⇒Q=24μC
Thus, the net charge in the circuit is Q=24μC
Now using the net charge and the value of capacitances at points A and B , we can find the potential at that point.
Potential at point A is VA=CQ=2μF24μC
⇒VA=12V
Potential at point B is VB=CQ=8μF24μC
⇒VB=3V
Now, that we know the potentials at points A and B , we have three potentials in the left side of the circuit between the points A and B
Applying Kirchhoff’s voltage law to the circuit, we get the potential difference between the points as
Vdiff=12+9+3V
⇒Vdiff=24V
Therefore, the potential difference between the points A and B is Vdiff=24V
Note: Ensure that all the quantities are in the same units or in SI units. Kirchhoff’s law states that if you travel around any loop in a circuit, the voltage across the elements add up to zero. Here, all the capacitors are connected in series and so the equivalent capacitance of the circuit will decrease. The voltage or potential difference is inversely proportional to the capacitance and so will increase if capacitance decreases.
