Question
Question: Five \[1\Omega \] resistances are connected as shown in the diagram. The resistance in the connectin...
Five 1Ω resistances are connected as shown in the diagram. The resistance in the connecting wires is negligible. The equivalent resistance between A and B is
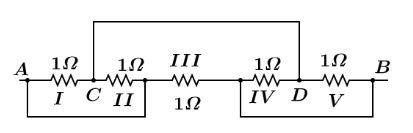
Solution
In electricity, resistance is the property of a material which opposes the flow of current through its and such electric components which shows this property called resistor. When resistors are connected in series their net resistance between two points can be calculated mathematically as Rseries=R1+R2+....+Rn and if these resistors are connected in parallel to each other, then net resistance between two points is calculated mathematically as Rparallel1=R11+R21+....+Rn1 hence, we will use these general formulas to find net resistance between point A and B in the given electric circuit.
Complete step by step answer:
The electrical circuit can also be reduced into its simple form as the resistors I(and)II are connected in series to each other. Resistors IV(and)V are connected in series,now these two series combination I(and)II and IV(and)V are connected in parallel with the resistor III , hence the reduced circuit can be drawn as:
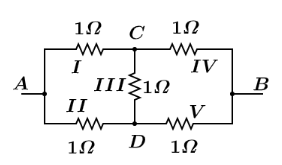
Now, Calculating net resistance of resistors I(and)II which are connected in series, of resistances R=1Ω
So, RI,II=1+1
RI,II=2Ω→(i)
Similarly, the combination IV(and)V are connected in series with resistance of R=1Ω
So, RIV,V=1+1
RIV,V=2Ω→(ii)
Now, the three combination of resistances RI,II=2Ω→(i) RIV,V=2Ω→(ii) and RIII=1Ω are all connected in parallel to each other,
So net resistance between points A and B is calculated by using the parallel formula
RAB1=RI,II1+RIV,V1+RIII1
⇒RAB1=21+21+11
⇒RAB1=2
⇒RAB=21Ω
∴RAB=0.5Ω
Hence, the equivalent resistance between point A and B is RAB=0.5Ω.
Note: It should be remembered that, when one resistors starting point is directly connected with the terminal point of another resistance it’s said to be resistances are connected in series, In series connection same current flows through each resistances whereas in parallel combination of resistances the current is not same but voltage across each resistances is same.
