Question

Find vertex of parabola: $x^2+7x-2$

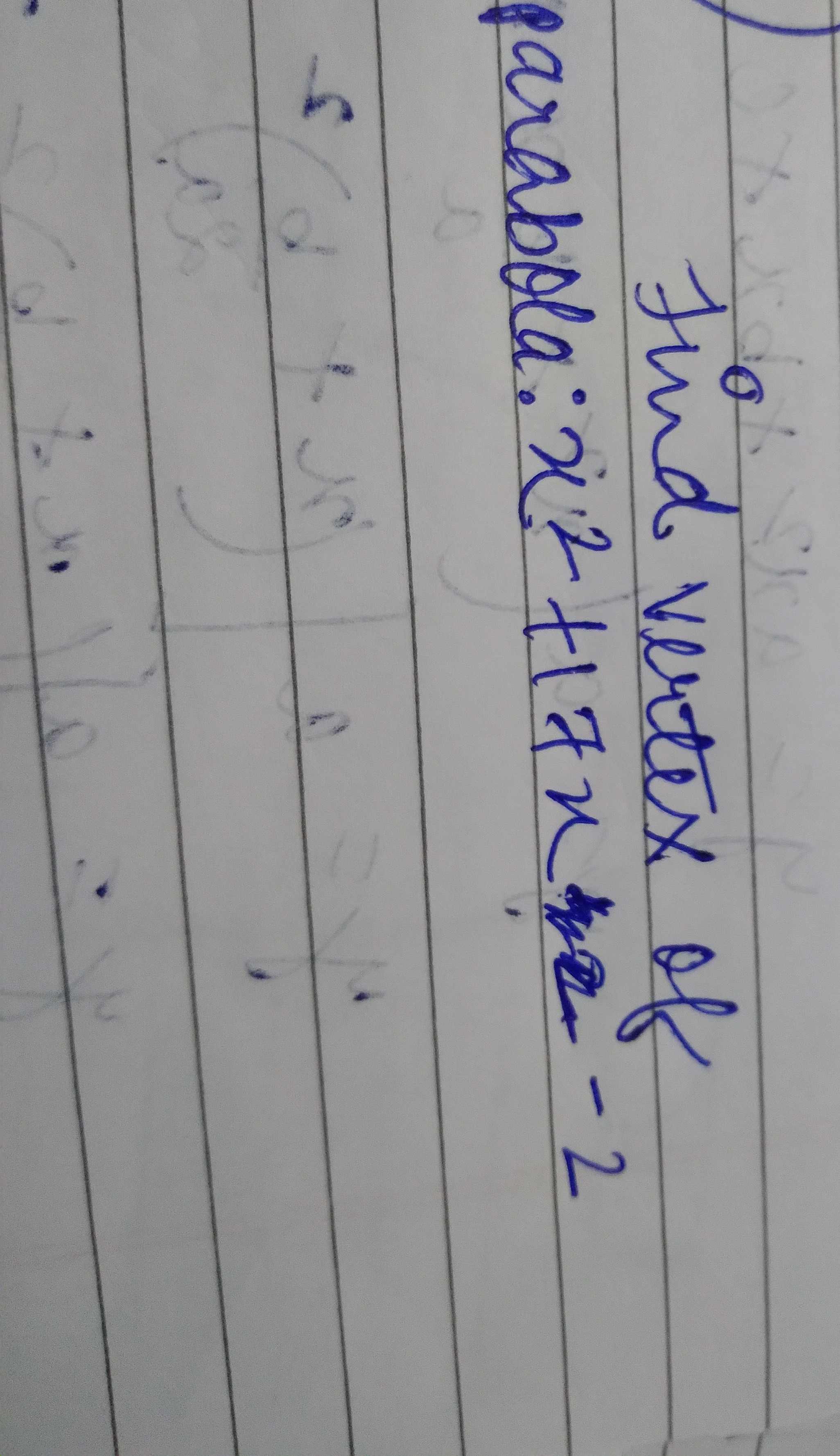
Answer 1

The vertex is $\left(-\frac{7}{2}, -\frac{57}{4}\right)$.

Answer 2

Assume the parabola equation is $y = x^2+7x-2$. For a parabola in the form $y = ax^2+bx+c$, the x-coordinate of the vertex is $x_v = \frac{-b}{2a}$. Here, $a=1$ and $b=7$. Thus, $x_v = \frac{-7}{2(1)} = -\frac{7}{2}$. Substitute this $x_v$ back into the equation to find $y_v$: $y_v = \left(-\frac{7}{2}\right)^2 + 7\left(-\frac{7}{2}\right) - 2 = \frac{49}{4} - \frac{49}{2} - 2 = \frac{49-98-8}{4} = -\frac{57}{4}$. The vertex is $\left(-\frac{7}{2}, -\frac{57}{4}\right)$.