Question

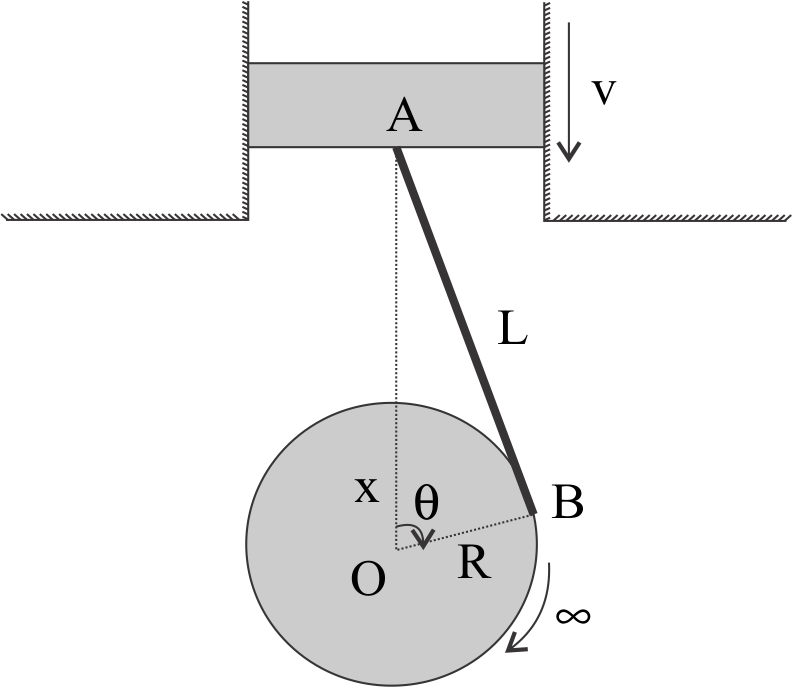
Find velocity of piston $A$ in the given situation if angular velocity of wheel of radius $R$ is $m$ (constant), in the clockwise sense. ( $O$ is a fixed point).

A) $\dfrac{{xR\omega \sin \theta }}{{R\cos \theta + x}}$
B) $\dfrac{{{x^2}\omega \sin \theta }}{{R\cos \theta - x}}$
C) $\dfrac{{xR\omega \sin \theta }}{{R\cos \theta - x}}$
D) $\dfrac{{{R^2}\omega \sin \theta }}{{R\cos \theta - x}}$

Answer 1

Velocity of piston is the change in displacement of piston with respect to time. So, first we will find an expression in terms of all given terms using some geometry. On differentiating the expression, we will find the expression in terms of velocity and angular velocity which will lead us to the expression for velocity.

Complete step by step solution:
In above $\Delta AOB$, $\angle ABO$ is $90^\circ$ (angle between tangent to a circle and it’s radius touching the tangent at circle’s circumference).
$\angle AOB$ is given to us as $\theta$
Let a triangle ABC with standard sides ${\text{a, b, c}}$ and standard angles ${\text{A, B, C}}$ in their standard positions, So, using property of triangle We know that,

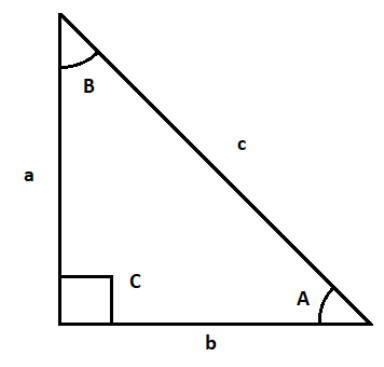
$\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$ and similarly for other angles,
So we can use the above $\cos$ property of triangle in $\Delta AOB$, so we gte,
$\cos \theta = \dfrac{{{R^2} + {x^2} - {L^2}}}{{2Rx}}$
Now we will differentiate this equation with respect to time.
Left side on differentiation:
$\dfrac{{d(\cos \theta )}}{{dt}} = - \sin \theta \dfrac{{d\theta }}{{dt}}$ -----(1)
Right side on differentiation:
$\dfrac{{d\left( {\dfrac{{{R^2} + {x^2} - {L^2}}}{{2Rx}}} \right)}}{{dt}} = \dfrac{{\left( {2Rx} \right)\left( {2x\dfrac{{dx}}{{dt}}} \right) - \left( {{R^2} + {x^2} - {L^2}} \right)\left( {2R\dfrac{{dx}}{{dt}}} \right)}}{{{{\left( {2Rx} \right)}^2}}}$
On simplification we get,
$\dfrac{{\left( {2Rx} \right)\left( {2x\dfrac{{dx}}{{dt}}} \right) - \left( {{R^2} + {x^2} - {L^2}} \right)\left( {2R\dfrac{{dx}}{{dt}}} \right)}}{{{{\left( {2Rx} \right)}^2}}} = \left( {\dfrac{{2R\left( {2{x^2} - {R^2} - {x^2} + {L^2}} \right)}}{{{{\left( {2Rx} \right)}^2}}}} \right)\left( {\dfrac{{dx}}{{dt}}} \right)$
On further simplification, we get,
$= \dfrac{{{x^2} + {L^2} - {R^2}}}{{2R{x^2}}}\dfrac{{dx}}{{dt}}$ --------(2)
Now equating equations $1$ and $2$, we get,
$- \sin \theta \dfrac{{d\theta }}{{dt}} = \dfrac{{{x^2} + {L^2} - {R^2}}}{{2R{x^2}}}\dfrac{{dx}}{{dt}}$ ----(3)
Now we know that, $\dfrac{{d\theta }}{{dt}} = \omega$ and $\dfrac{{dx}}{{dt}} = v$
Where $v$ is velocity.
So, on simplifying, we get equation $3$ as,
$- \sin \theta \times \omega = \dfrac{{{x^2} + {L^2} - {R^2}}}{{2R{x^2}}} \times v$
On simplifying, we get,
$v = - \dfrac{{2R{x^2}\omega \sin \theta }}{{{x^2} + {L^2} - {R^2}}}$
Now, using Pythagoras theorem in $\Delta AOB$, we get,
${L^2} = {x^2} - {R^2}$
Using above equation in expression of velocity we get,
$v = - \dfrac{{2R{x^2}\omega \sin \theta }}{{{x^2} + {x^2} - {R^2} - {R^2}}}$
On simplification we get,
$v = - \dfrac{{R{x^2}\omega \sin \theta }}{{{x^2} - {R^2}}}$
Now, using trigonometric ratio of cos in $\Delta AOB$, we get,
$R = x\cos \theta$
So we get velocity expression on simplification as,
$v = - \dfrac{{R{x^2}\omega \sin \theta }}{{{x^2} - Rx\cos \theta }}$
On further simplification, we get,
$v = \dfrac{{xR\omega \sin \theta }}{{R\cos \theta - x}}$

So the correct answer is option (C).

Note: We were able to find velocity in this way because angular velocity was constant, otherwise, practically, angular velocity of the piston would have increased. This question was all about mathematics and a little bit of physics. You just have to adapt your solution in the form of options using suitable mathematical properties.