Question

Find value of Q from following equations.

(i) $C_{(s)}+O_{2(g)} \longrightarrow CO_{2(g)} \Delta H = QkJ$ (ii) $C_{(s)}+\frac{1}{2}O_{2(g)} \longrightarrow CO_{2(g)} \Delta H = 2xkJ$ (iii) $C_{(s)}+\frac{1}{2}O_{2(g)} \longrightarrow CO_{2(g)} \Delta H = 2y kJ$

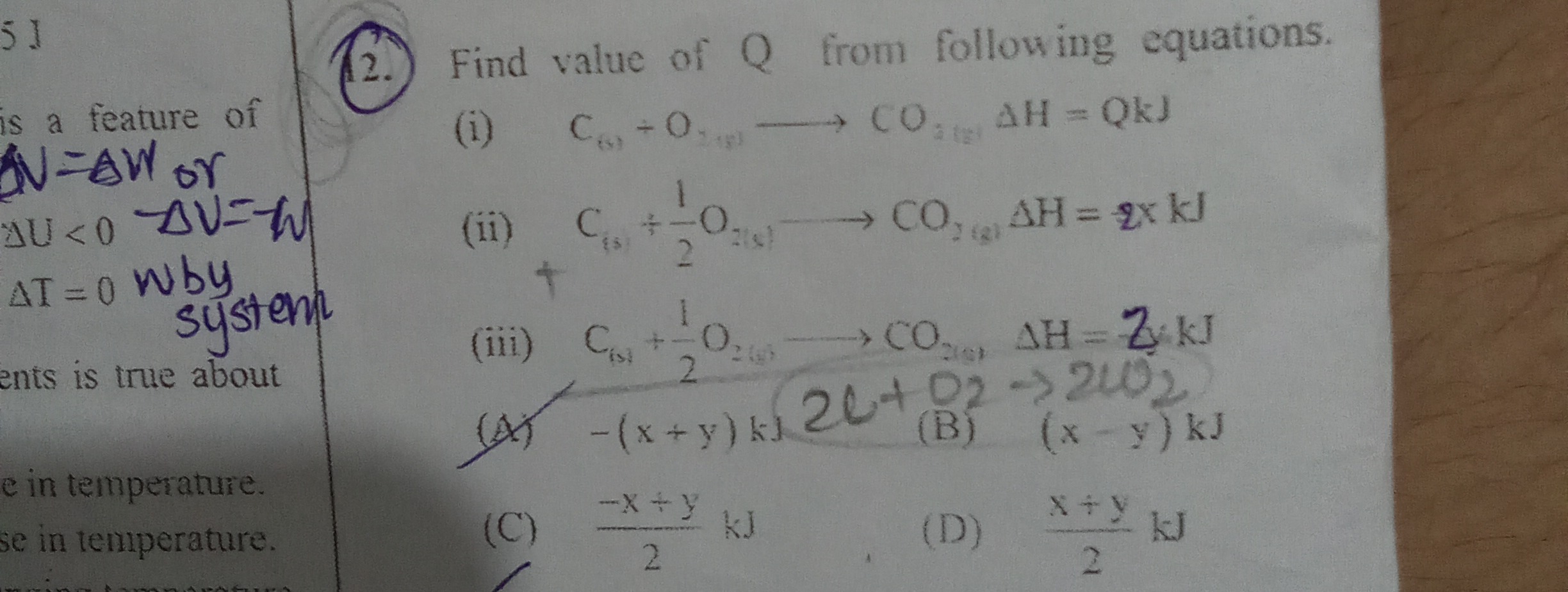
• A. -(x+y) kJ
• B. (x-y) kJ
• C. $\frac{-x+y}{2} kJ$
• D. $\frac{x+y}{2} kJ$

Answer 1

Answer: (A)

-(x + y) kJ

Answer 2

Solution:

For the formation reaction

$C_{(s)} + \frac{1}{2}O_{2(g)} \longrightarrow CO_{2(g)}$

the two experiments yield the energy changes 2x kJ and 2y kJ. Interpreting these as corresponding to –x kJ and –y kJ per mole (after accounting for the sign convention), we take the average for the half–reaction:

$\Delta_{1/2} = -(x + y)/2$

Now, the full reaction,

$C_{(s)} + O_{2(g)} \longrightarrow CO_{2(g)}$

is exactly twice the half–reaction so that

$Q = 2 \times [-(x + y)/2] = -(x + y) kJ$