Question

Find the y-coordinate of the focus of this lens system.

(A) $\dfrac{{\left( {{f_1} + d} \right)\Delta }}{{\left( {{f_1} + {f_2} - d} \right)}}$
(B) $\dfrac{{2\left( {{f_1} - d} \right)\Delta }}{{\left( {{f_1} + {f_2} + d} \right)}}$
(C) $\dfrac{{2\left( {{f_1} - d} \right)\Delta }}{{\left( {{f_1} + {f_2} + d} \right)}}$
(D) $\dfrac{{\left( {{f_1} - d} \right)\Delta }}{{\left( {{f_1} + {f_2} - d} \right)}}$

Answer 1

Hint For solving this question, we need to place the object at the infinite distance from the lens system. Then, with the application of the lens formula, and the magnification formula for the lens, we need to determine the height of the final image, which will be the y-coordinate of the focus of the lens system.

Formula Used: The formulae used in this solution are:
$\Rightarrow \dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
$\Rightarrow m = \dfrac{v}{u}$
where $m$ is the magnification produced, $f$ is the focal length, $v$ is the image distance, and $u$ is the object distance from the lens.

Complete step by step answer
We know that the image of the object placed at an infinite distance from a lens is formed at the focus of the lens. So, we place our object at an infinite distance from this lens system, so that the final image forms at the focus of the lens system.
We treat both the lens as a single system and place the object at infinity.
As the object distance from the centre of lens is infinity, this lens forms the image at its focus, that is, at a distance of ${f_1}$ from the first lens.
Now, this image ${I_1}$ formed at the focus of the first lens acts as an object for the second lens.
For the second lens:
Distance of ${I_1}$ from the second lens $= d - {f_1}$
Substituting $f = {f_2}$ and $u = - \left( {d - {f_1}} \right)$ we get
$\Rightarrow \dfrac{1}{{{f_2}}} = \dfrac{1}{v} - \dfrac{1}{{ - \left( {d - {f_1}} \right)}}$
$\Rightarrow \dfrac{1}{v} = \dfrac{1}{{{f_2}}} - \dfrac{1}{{\left( {d - {f_1}} \right)}}$
Taking the LCM
$\Rightarrow \dfrac{1}{v} = \dfrac{{\left( {d - {f_1}} \right) - {f_2}}}{{{f_2}\left( {d - {f_1}} \right)}}$
Taking reciprocal, we get
$\Rightarrow v = \dfrac{{{f_2}\left( {d - {f_1}} \right)}}{{d - \left( {{f_1} + {f_2}} \right)}}$
Now, we know that the magnification produced by a lens is given by
$\Rightarrow m = \dfrac{{\dfrac{{{f_2}\left( {d - {f_1}} \right)}}{{d - \left( {{f_1} + {f_2}} \right)}}}}{{ - \left( {d - {f_1}} \right)}}$
Cancelling $\left( {d - {f_1}} \right)$ from the numerator and the denominator, we get
$\Rightarrow m = - \dfrac{{{f_2}}}{{d - \left( {{f_1} + {f_2}} \right)}}$ (1)
Now, let the height of the final image $\left( I \right)$ be $h'$ with respect to the second lens.

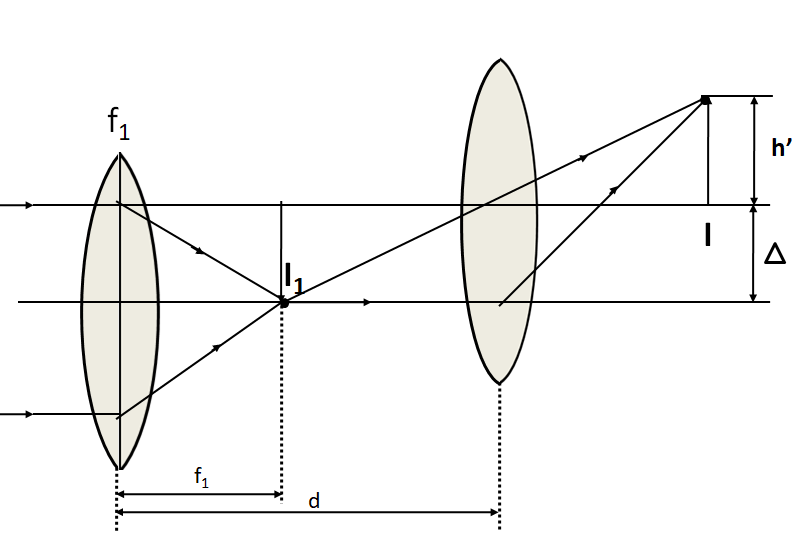
As the centre of the second lens is at a distance $\Delta$ above the centre of the first lens, so the height of the object, $h = - \Delta$
We know that the magnification is also given by
$\Rightarrow m = \dfrac{{h'}}{h}$
$\Rightarrow m = \dfrac{{h'}}{{ - \Delta }}$
Substituting from (1)
$\Rightarrow - \dfrac{{{f_2}}}{{d - \left( {{f_1} + {f_2}} \right)}} = \dfrac{{h'}}{{ - \Delta }}$
Multiplying with $- \Delta$ on both the sides, we get
$\Rightarrow h' = \dfrac{{\Delta {f_2}}}{{d - \left( {{f_1} + {f_2}} \right)}}$
Now, this is the height of the image with respect to the second lens. For getting the y-coordinate of the focus of this lens system, we have to determine the height of the final image with respect to the first lens.
As the first lens is at a distance of $\Delta$ below the second lens, so the height of the final image with respect to the first lens
$\Rightarrow y = h' + \Delta$
$\Rightarrow y = \dfrac{{\Delta {f_2}}}{{d - \left( {{f_1} + {f_2}} \right)}} + \Delta$
Taking $\Delta$ common, we get
$\Rightarrow y = \Delta \left( {\dfrac{{{f_2}}}{{d - \left( {{f_1} + {f_2}} \right)}} + 1} \right)$
Taking the LCM
$\Rightarrow y = \Delta \left( {\dfrac{{{f_2} + d - {f_1} - {f_2}}}{{d - \left( {{f_1} + {f_2}} \right)}}} \right)$
$\Rightarrow y = \dfrac{{\Delta \left( {d - {f_1}} \right)}}{{d - \left( {{f_1} + {f_2}} \right)}}$
Multiplying the numerator and denominator by $- 1$ , we get
$\Rightarrow y = \dfrac{{\left( {{f_1} - d} \right)\Delta }}{{\left( {{f_1} + {f_2} - d} \right)}}$
This is the height of the final image with respect to the first lens. As the object is placed at an infinite distance from the first lens, so this is equal to the y-coordinate of the lens system.

Note
Do not get confused from which lens the height of the final image must be taken. As the light ray is incident on the surface of the first lens, so we must take the height with respect to this lens only. Also, take proper care of the sign convention for the image and the object distances from the lens before putting them into the lens and the magnification formula.