Question

Find the work done when the point charge of $2\mu C$ is moved from a point at a potential of $- 10V$ to a point at which potential is zero.

Answer 1

This problem is based on the electric potential, electrical potential is defined as the amount of work done bringing the charge from one point to the other point. Therefore potential difference is the product of the charge and change in potential difference. Here the potential at a point is given as $- 10V$ and whereas the potential at the point where we need to bring the charge is zero and the charge is given as $2\mu C$.

Formula used:
$W = q\left( {{V_A} - {V_B}} \right)$
Where $W =$ Work done, $q =$ Magnitude of charge, ${V_A}$ and ${V_B}$ is the potential at point $A$ and $B$ respectively.

Complete step by step answer:
The potential difference can also be defined as the amount of work done by an external force in moving a unit positive charge slowly or without acceleration from one point to the other point in an electrostatic field. If the system contains a group of charges then electric potential due to the group of charges at a given point is the algebraic sum of the potential due to individual charges.

Given: $q = 2\mu C = 2 \times {10^{ - 6}}\,C$
${V_A} = 0\,V$
$\Rightarrow {V_B} = - 10\,V$

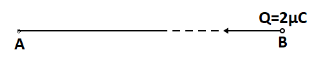
Here the charge $2\mu C$ is placed at point $B$ which has potential difference of $- 10V$ and zero potential difference at point $A$
We know that,
Work done $W = q\left( {{V_A} - {V_B}} \right)$ ……… $\left( 1 \right)$
Substituting the given values in above equation,
$W = 2 \times {10^{ - 6}}\left( {0 - \left( { - 10} \right)} \right)$
On simplifying the above equation we get,
$W = 2 \times 10 \times {10^{ - 6}}$
$\Rightarrow W = 20 \times {10^{ - 6}}$
Therefore work done is,
$\therefore W = 2 \times {10^{ - 5}}\,J$

Hence the work done to bring the charge is $2 \times {10^{ - 5}}\,J$.

Note: The potential difference and work both are scalar quantities. Therefore potential differences and work have only magnitude and no direction. The S.I unit for potential difference and work is volts $\left( V \right)$ and joules $\left( J \right)$ respectively. In the questions involving potential difference, we must remember while substituting the values of initial and final potential that point $A$ represents the final position and point $B$ represents the initial position. To avoid the confusion, we must remember that the difference is the initial position subtracted from the final position.