Question

Find the work done by tension on 1 kg block when the 4kg block moves down by 1m after the system is released. All surfaces are frictionless & strings are ideal :-

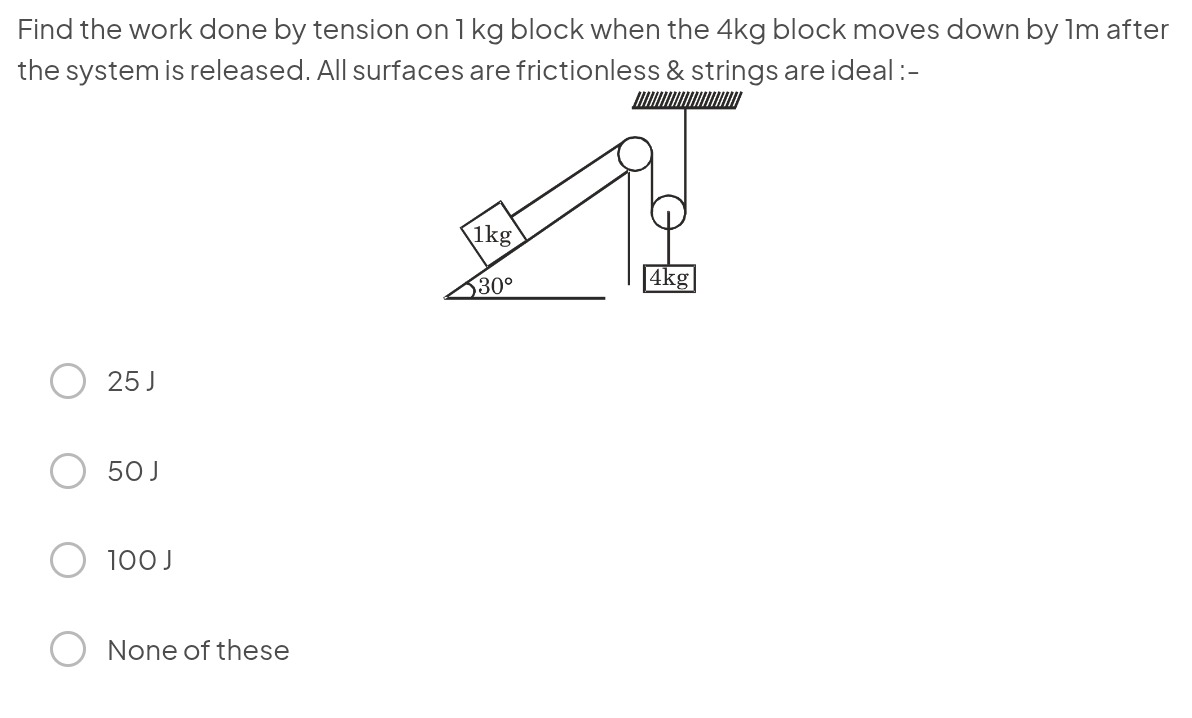
• A. 25 J
• B. 50 J
• C. 100 J
• D. None of these

Answer 1

Answer: (A)

25 J

Answer 2

The problem involves a system of two blocks connected by strings and pulleys. We need to find the work done by tension on the 1 kg block when the 4 kg block moves down by 1 meter.

1. Kinematic Relationship: Let $x$ be the distance the 1 kg block moves up the incline and $y$ be the distance the 4 kg block moves down. The pulley system is such that for every distance $y$ the 4 kg block moves down, the length of the string from the fixed pulley to the movable pulley increases by $y$, and the length of the string from the movable pulley to the ceiling attachment also increases by $y$. This means the total length of string that must be pulled from the other side is $2y$. Therefore, the 1 kg block moves up the incline by $x = 2y$. Given that the 4 kg block moves down by $y = 1$ m, the 1 kg block moves up the incline by $x = 2 \times 1 = 2$ m.

2. Equations of Motion: Let $T$ be the tension in the string. Let $a_4$ be the acceleration of the 4 kg block downwards and $a_1$ be the acceleration of the 1 kg block up the incline. From the kinematic relationship, $a_1 = 2a_4$.

   • For the 4 kg block: The forces are its weight ($4g$) downwards and twice the tension ($2T$) upwards (since the movable pulley is supported by two segments of the string with tension $T$). Equation of motion: $4g - 2T = 4a_4$.
   • For the 1 kg block: The forces are tension ($T$) up the incline and the component of gravity down the incline ($1g \sin 30^\circ$). Equation of motion: $T - 1g \sin 30^\circ = 1a_1$. Since $\sin 30^\circ = 1/2$, this becomes $T - \frac{g}{2} = a_1$.

3. Solving for Tension: Substitute $a_1 = 2a_4$ into the second equation: $T - \frac{g}{2} = 2a_4$. From the first equation, we can express $2a_4$ as: $2a_4 = 2g - T$. Substitute this into the modified second equation: $T - \frac{g}{2} = 2g - T$. Rearranging the terms to solve for $T$: $2T = 2g + \frac{g}{2} = \frac{5g}{2}$. $T = \frac{5g}{4}$.

4. Work Done by Tension: The work done by tension on the 1 kg block is given by $W = T \times x$, where $T$ is the tension and $x$ is the displacement of the block in the direction of the tension. The tension $T$ acts up the incline, and the 1 kg block moves up the incline by $x = 2$ m. $W = T \times x = \left(\frac{5g}{4}\right) \times 2 = \frac{5g}{2}$. Assuming $g = 10 \, \text{m/s}^2$ (standard value for JEE/NEET problems unless specified otherwise): $W = \frac{5 \times 10}{2} = \frac{50}{2} = 25 \, \text{J}$.