Solveeit Logo
Login

Question

Question: Find the work done by a gas when it expands isothermally at \[37^\circ {\text{C}}\] to four times it...

Find the work done by a gas when it expands isothermally at 37∘C37^\circ {\text{C}} to four times its initial volume.
A 3753  J  3753\;{\text{J}}\;
B 3573  J  3573\;{\text{J}}\;
C 7533  J  7533\;{\text{J}}\;
D 5375  J5375\;{\text{J}}

Explanation

Solution

In this question, first draw the pressure vs volume curve of an isothermal process and discuss the work done by this process. Apply the condition of final volume and initial volume to find out the work done.

Complete step by step solution:
In this problem, the gas is expanding isothermally at 37∘C37^\circ {\text{C}} means the temperature remains constant and the volume of the gas changes four times the initial volume. We have to calculate the amount of force required to expand the gas.
Now, we consider the p−vp - v diagram of the Isothermal process as,

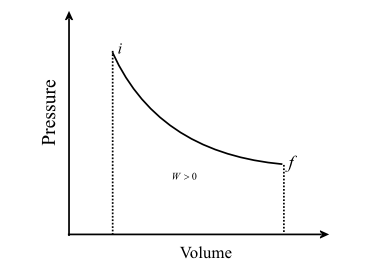
Let us assume v1{v_1} is initial volume and so according to the given condition and v2{v_2} Is the final volume.
Let WW be the total work done, so for the isothermal process we can write
W = nRTlnv2v1W{\text{ }} = {\text{ }}nRTln\dfrac{{{v_2}}}{{{v_1}}}
As we know, here the universal gas constant is RR, the temperature of the process is TT, and the number of moles is nn
According to the given condition, we can write
v2 = 4v1{v_2}{\text{ }} = {\text{ }}4{v_1}
First we convert the unit of the temperature from ∘C^\circ {\text{C}} to Kelvin{\text{Kelvin}} as,
T=(37∘C+273)  KT = \left( {37^\circ {\text{C}} + 273} \right)\;{\text{K}}
⇒T=310  K\Rightarrow T = 310\;{\text{K}}
Now, we substitute the given values in the work done expression as,
W = (1)(8.314)(310)ln(4)W{\text{ }} = {\text{ }}\left( 1 \right)\left( {8.314} \right)\left( {310} \right){\text{ln}}\left( 4 \right)
After simplification we obtain,
∴W=3573  J\therefore W = 3573\;{\text{J}}

Thus, the work done by a gas when it expands isothermally at 37∘C37^\circ {\text{C}} to four times its initial volume is 3573  J3573\;{\text{J}}.

Note: As we know that if the system is compressed by the surrounding, then the work done is negative and the internal energy of the system increases. And if the system expands, it will work on the surroundings and the internal energy of the system decreases.