Question

Find the vertical and horizontal component.

Answer 1

In order to solve this question, we should know about trigonometric ratios and here we have given a vector which is making an angle of ${76^o}$ with a line and the magnitude of vector is also given to us so, we have to resolve its components along horizontal and vertical direction which we will find by using trigonometric ratios in a right angle triangle.

Formula used: In a right angle triangle, if one of the angle is $\theta$ then useful trigonometric ratios are defined as
$\cos \theta = \dfrac{a}{c}$ where a denotes the side adjacent to the angle and c denotes the hypotenuse side.
$\sin \theta = \dfrac{b}{c}$ where b denotes the side opposite to the angle.

Complete step by step solution:
According to the question, we have given the magnitude of a vector V as $V = 31.0$ and the angle made by it with a line is $\theta = {76^o}$ now, let us draw the complete diagram to make a right angle triangle and horizontal and vertical component of the vector V are shown in the diagram as

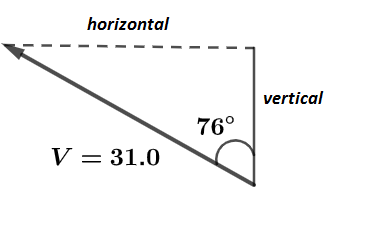
So, for vertical component we will use cosine of the angle made but horizontal component line so,
$\cos \theta = \dfrac{{{V_v}}}{{hypotenuse}}$ where hypotenuse of this right angle triangle has a value of $31$ and we know that $\cos 76 = 0.24$ on putting these values we get,
$0.24 = \dfrac{{{V_v}}}{{31}}$
$\Rightarrow {V_v} = 7.5$
and similarly for vertical component from the diagram we have,
$\sin \theta = \dfrac{{{V_h}}}{{hypotenuse}}$ and we know that, $\sin 76 = 0.97$ so, on putting the values we get,
${V_h} = 0.97 \times 31$
$\Rightarrow {V_h} = 30.07$
Hence, the horizontal and vertical components of given vectors are ${V_v} = 7.5$ and ${V_h} = 30.07$.

Note:
It should be remembered that, while using trigonometric ratios, always check the adjacent side is one with which hypotenuse makes an angle and here, the vector’s magnitude has not any units so, we simply write in terms of numerical values, a vector can represent either velocity, acceleration or any other vector physical quantity.