Question

Find the vertex, focus and sketch ${x^2} + 8y = 0$?

Answer 1

We transform the given equation into an equation similar to the equation of parabola. Comparing the equation formed with the general equation of parabola we find the vertex and focus. Calculate the points for sketching the graph and plot it on the graph.
The general quadratic equation of parabola with vertex as origin i.e. $(0,0)$ and focus $(0,p)$ is $y = \dfrac{1}{{4p}}{x^2}$.

Complete step by step answer:
We are given the equation ${x^2} + 8y = 0$
We shift one value to right side of the equation
$\Rightarrow 8y = - {x^2}$
Divide both sides of the equation by 8
$\Rightarrow y = \dfrac{{ - 1}}{8}{x^2}$ -----(1)
We compare the equation on right hand side to the general equation of parabola having vertex as origin i.e. $(0,0)$ and focus $(0,p)$ is $y = \dfrac{1}{{4p}}{x^2}$
$\dfrac{{ - 1}}{8} = \dfrac{1}{{4p}}$ then $p = - 2$
So, the vertex is $(0,0)$ and focus is $(0, - 2)$
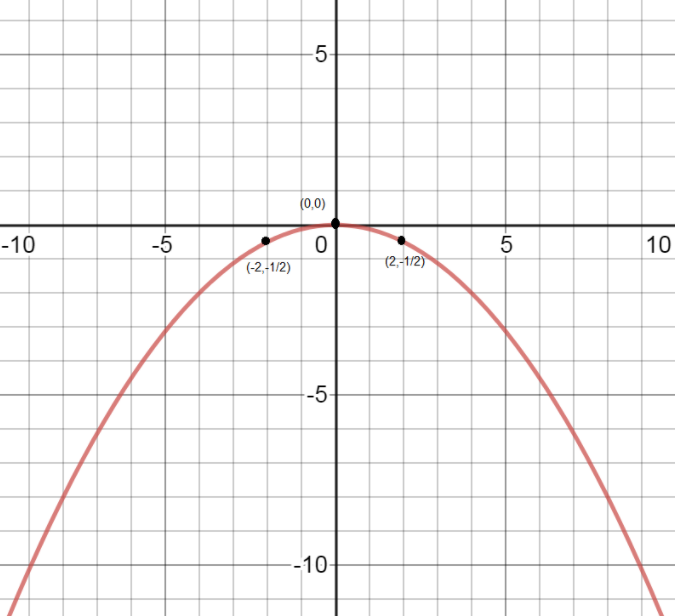
Now we plot the graph of the function ${x^2} + 8y = 0$ by substituting points
We put $x = 0$ in the equation, then $y = 0$
So, the point becomes $(0,0)$
Now we put $x = - 2$ in the equation, then $y = \dfrac{{ - 1}}{2}$
So, the point becomes $\left( - 2,\dfrac{{ - 1}}{2}\right)$
Now we put $x = 2$ in the equation, then $y = \dfrac{{ - 1}}{2}$
So, the point becomes $\left(2,\dfrac{{ - 1}}{2}\right)$
We will mark the points $(0,0)$, $\left( - 2,\dfrac{{ - 1}}{2}\right)$ and $\left(2,\dfrac{{ - 1}}{2}\right)$ on the graph. Also, we know that the equation in the question is equation of parabola as it is similar to general equation of parabola i.e. $y = \dfrac{1}{{4p}}{x^2}$.

Note: Writing the coordinates wrong as here y is given in place of $f(x)$, keep in mind the function is dependent on x and we will write the value of y as value of the function obtained by putting in the value of x. Also, students should be aware of the fact that whenever they see a quadratic equation, it must be an equation for the parabola so you don’t have to plot all the points.