Question
Question: Find the vertex, focus and directrix of the parabola. Then sketch its graph. \(4x - {y^2} - 2y - ...
Find the vertex, focus and directrix of the parabola. Then sketch its graph.
4x−y2−2y−33=0
Solution
Here we will convert the given equation into a standard form of parabola. The standard form of parabola is given as: (y−k)2=4a(x−h). After converting, we will compare with the standard form and find the vertex (h, k), length of latus rectum (4a) and equation of directrix for the given equation and finally draw the graph.
Complete step-by-step answer:
The given Equation is:
4x−y2−2y−33=0
We can rewrite it as,
y2+2y=4x−33
On adding and subtracting 1 on left hand side, we get:
y2+2y+1−1=4x−33
We know that (a2+b2+2ab)=(a+b)2. So the above expression can be written as:
(y+1)2−1=4x−33
⇒(y+1)2=4x−32
On taking the 4 common from RHS, we get:
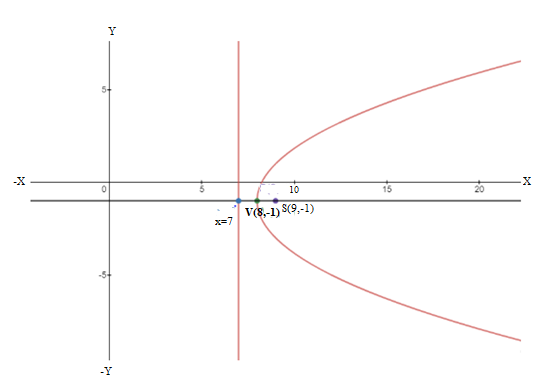
(y+1)2=4(x−8) (1)
We know that the general form of a parabola is given as: (y−k)2=4a(x−h), where (h, k) is the vertex and 4a is the length of the latus rectum.
And the equation of directrix is given as: x + a –h =0.
Therefore, on comparing the equation 1 with the general equation of parabola, we get:
Vertex (h, k) = (8, -1)
4a = 4 = length of latus rectum.
And the equation of directrix is
x + a –h =0.
On putting the value of a and h, we have:
x+1−8=0
⇒x−7=0
Therefore, the vertex for the given parabola is (8, -1) and the length of the latus rectum is 4 and the directrix is x – 7 =0.
Thus the graph would be:
Note: To solve these kinds of questions, you should convert the given equation in some standard form and then compare the given equation with the general equation of the curve to find some prominent points like vertex and focus to plot the graph. You should also know that focus is at (h + a, k) for the parabola (y−k)2=4a(x−h).
