Question
Question: Find the velocity of the projectile at the highest point, if it is projected with a speed \(15\;m\;{...
Find the velocity of the projectile at the highest point, if it is projected with a speed 15ms−1, in the direction 45∘ above horizontal. [take g=10ms−2]
Solution
Hint We know that a projectile is an object upon which the only force is the gravity. Gravity has an influence on the vertical motion of the projectile, thus there occurs a vertical acceleration. Based on this concept we have to solve this question.
Step-by step answer
To start this question we should be knowing the diagram for the better understating. So, here it is:
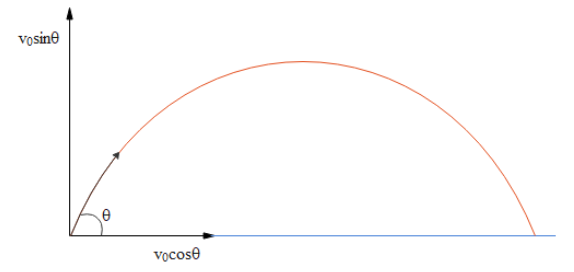
Initially we can say that:
VY(invertical)=15sin45∘=215
VK(inhorizontal)=15cos45∘=215
So, we can say that:
Height point VV(inhorizontal)=15cos45∘=215.
Hence, the answer is 15cos45∘=215.
The value is given as 10.6 m/sec.
Note: To solve this question we should know that the horizontal motion of the projectile is the result of the tendency of any object in the motion to remain in the motion which is the constant velocity. Real life examples of projectile motions are throwing a ball or a cannonball, the motion of a boat in a river, the motion of the earth around the sun the motion of a shell fired from a gun, etc,.
