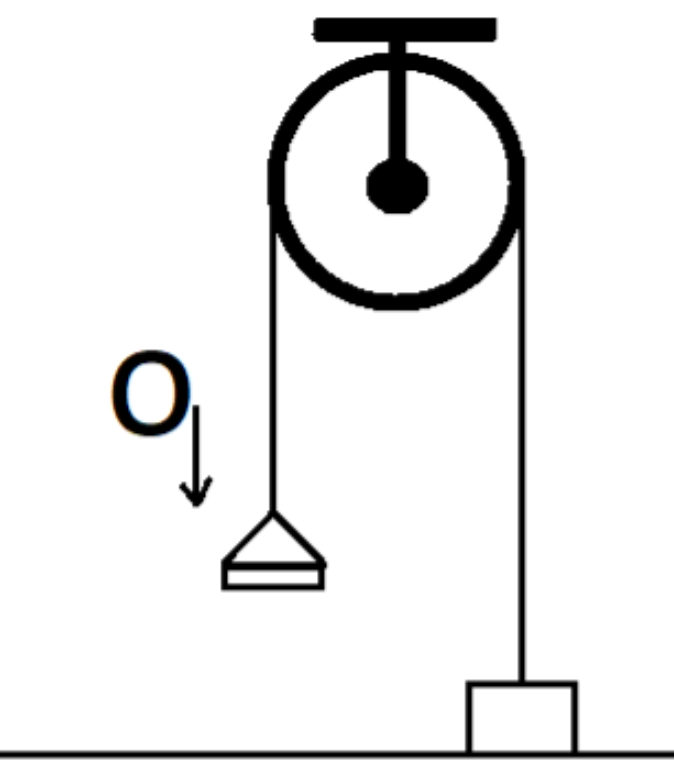
Question

Find the velocity of the pan + ball system at t = 2.6 s. Assume that the block comes to rest instantaneously after striking the floor

A. 4 m/s downwards
B. 0.6 m/s upwards
C. 4 m/s upwards
D. 0.4 m/s downwards

Answer 1

This question can be solved by the concept of impulse. In classical mechanics, the impulse (symbolised by I or Imp) is the integral part of a force for which it functions over the time interval. Since force is a quantity of vectors, impulse is a quantity of vectors as well. An object's impulse induces an analogous vector shift in its linear momentum, often in the same direction.

Complete step by step answer:
Before we start solving the given question, let us take a look at all the parameters that are given to us.
GIVEN PARAMETERS
Let the mass of ball be,
​${{m}_{0}}$ = 0.5 kgs
Now, mass block
M = 3 kg
And, mass of pan
m = 1.5 kg
${{v}_{0}}$ = 20 m/s
Now,
As the string is inextensible the velocity of all the masses will be same
Also,
v is the final velocity of each mass.
Now,
Impulse on the ball,
$I=\Delta P$
$\Rightarrow I={{m}_{0}}\left( {{v}_{0}}-v \right)$
$\Rightarrow I=0.5\left( 20-v \right)$ ……………………(1)
And, impulse on the block
${{I}_{1}}=Mv=3v$ ……………………(2)
Impulse on the pan,
$I-{{I}_{1}}=mv=1.5v$
Now, substituting the values from equations (1) and (2)
We have,
$\Rightarrow 10-0.5v-3v=1.5v$
$\Rightarrow 5v=10$
We have,
the final velocity,
v = 2m/s in upward direction.
Let the tension acting on the string be T
So,
Mg – T = Ma
$\Rightarrow 30\text{ }\text{ -}T\text{ }=3a$ ……………………..(4)
Also,
$T-20=2a$ ……………………..(5)

By adding equation (4) and (5), we get
$30-T+T-20=3a+2a$
$\Rightarrow 5a=10$
So, we have
$a=2m/{{s}^{2}}$
So,
Before the jerk, the velocity of the mass is
v = 2m/s
and,
After the jerk, the velocity of the block is u.
Impulse on block is
${{I}_{1}}=3u$
$\Rightarrow {{I}_{1}}=\Delta P=2\left( 2-u \right)$
So,
Using the values from above
$\Rightarrow 3u=2\left( 2-u \right)$
$\Rightarrow 3u=4-2u$
$\Rightarrow 5u=4$
$\Rightarrow u=\dfrac{4}{5}$
$\Rightarrow u=0.8m/s$
Velocity of each masses will be
u = 0.8 m/s
So,
Block goes down with velocity v after 2.4 seconds and accelerates in the upward direction with $2m/{{s}^{2}}$
Equation of motion,
v = u + at
$\Rightarrow v\text{ }=\text{ }0.8-2\times 0.2$
So, we have
$v\text{ }=0.4m/s$ Downward.
So, the velocity of pan + ball system at t = 2.6 s will be
$\therefore$ $v\text{ }=0.4m/s$ Downward.

So, the correct answer is “Option D”.

Note: Examples of incorporating the principle of impulse to minimise the force of impact are automotive airbags and cushioned gymnasiums. The force on a tennis ball is improved by providing great racquet head speed. This reduces the impact time between the ball and the racquet, thereby increasing the impact force.