Question
Question: Find the velocity of the center of mass C and the angular velocity of the system about the center of...
Find the velocity of the center of mass C and the angular velocity of the system about the center of mass after the collision.
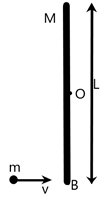
Solution
We need to understand the given situation in which two bodies are moving, then collides and eventually sticks together and travels with a center of mass. We can find the relation between the given parameters to get the required solution.
Complete answer: We are given a point mass ‘m’ and a rod of mass ‘M’. The point mass is moving perpendicular to the rod which is initially at rest and collides at one end of the rod.
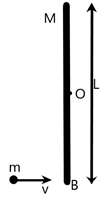
As a result of this collision, the point mass sticks to the rod and both undergo a motion along the center of mass of the system.

The length of the rod is given to be of ‘L’ units. So, we can find the position of the center of mass of the system ‘x’ from the origin O, which is the center of the rod as –
