Question

Find the vector equation of the coordinate planes.

Answer 1

We know that for a XY plane z coordinate is 0, for an YZ plane x coordinate is 0 and for a ZX plane y coordinate is 0.

Complete step-by-step answer:
Observe the figure given below.

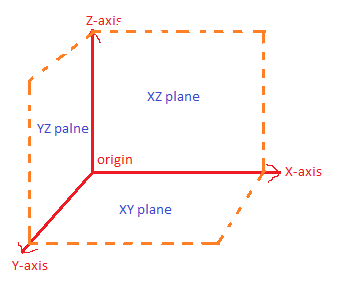
From the figure above we observe that the Z-axis is perpendicular to the XY plane, Y-axis is perpendicular to the XZ plane and X-axis is perpendicular to YZ plane.
Let $\vec r = a\mathop i\limits^ \wedge + b\mathop j\limits^ \wedge + c\mathop k\limits^ \wedge$ is a position vector in the plane.
Let $\mathop i\limits^ \wedge$ be the unit vector parallel to the X-axis, $\mathop j\limits^ \wedge$ be the unit vector parallel to the Y-axis and $\mathop k\limits^ \wedge$ be the unit vector parallel to Z-axis respectively.

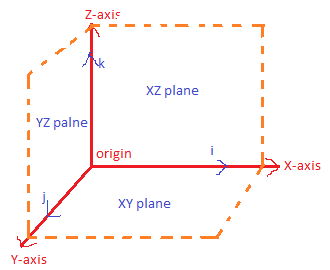
For an XY plane:
Unit vector parallel to the z axis is normal to the plane. That is their dot product with XY plane is equal to zero. So the equation of the plane is $\vec r.\mathop k\limits^ \wedge = 0$ or we know that a point lying on this plane has z coordinate is 0. So the equation can also be written as $\vec r = a\mathop i\limits^ \wedge + b\mathop j\limits^ \wedge$.
Similarly for the other two planes we can write.
For an YZ plane:
Unit vector parallel to the x axis is normal to the plane. That is, their dot product with the YZ plane is equal to zero. So the equation of the plane is $\vec r.\mathop i\limits^ \wedge = 0$ or we know that a point lying on this plane has x coordinate is 0. So the equation can also be written as $\vec r = b\mathop j\limits^ \wedge + c\mathop k\limits^ \wedge$.
For an XZ plane:
Unit vector parallel to the z axis is normal to the plane. That is their dot product with XY plane is equal to zero. So the equation of the plane is $\vec r.\mathop j\limits^ \wedge = 0$ or we know that a point lying on this plane has z coordinate is 0. So the equation can also be written as $\vec r = a\mathop i\limits^ \wedge + c\mathop k\limits^ \wedge$.
Note: Note that a dot product of a position vector with unit vector parallel to the plane is taken zero here because there is an angle of ${90^ \circ }$ in between them. Unit vector is having value 1.