Question

Find the values of $\theta$ and p, if the equation $xcos\theta +ysin\theta =p~$ is the normal form of the line $\sqrt{3}x+y+2=0$

Answer 1

In geometry, a line can be defined as a straight one- dimensional figure that has no thickness and extends endlessly in both directions. It is often described as the shortest distance between any two points.

Complete step-by-step solution
The equation of the straight line upon which the length of the perpendicular from the origin is p and this perpendicular makes an angle α with the x-axis is $x\cos \alpha +y\sin \alpha =p$.
In the below diagram, we have shown the equation of a line $x\cos \alpha +y\sin \alpha =p$.

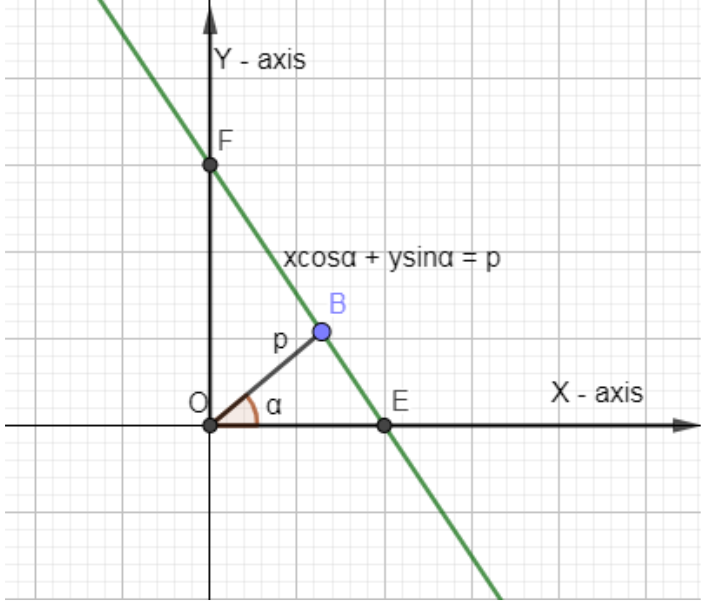
If the line length of the perpendicular drawn from the origin upon a line and the angle that the perpendicular makes with the positive direction of the x-axis be given then to find the equation of the line.
This is the normal form of a line.
As mentioned in the question, we have to find the values of $\theta$ and p for the given line when it is converted into the normal form of a line.
Now, to convert the given equation into the normal form, we can do the following:-
Firstly, we will divide the equation that is both sides of the equation with 2, and then we will observe the equation that is obtained as follows
$-\dfrac{\sqrt{3}}{2}x-\dfrac{1}{2}y=1$
Now, we can observe that the coefficients of x and y can be converted as sin and cos form as follows

& x\cos \left( \pi +\dfrac{\pi }{6} \right)+y\sin \left( \pi +\dfrac{\pi }{6} \right)=1 \\\ & x\cos \dfrac{7\pi }{6}+y\sin \dfrac{7\pi }{6}=1 \\\ \end{aligned}$$ **Now, on comparing this equation with the normal form of a line, we get the following result as $$\theta =\dfrac{7\pi }{6}$$ and p=1.** **Note:** The mistake that you could make is that even after writing $$\sqrt{3}x+y+2=0$$ in the form of $$xcos\theta +ysin\theta =p~$$, you might be wrong if you don’t know the value of $\cos \theta \And \sin \theta $ lies from -1 to 1. Rewriting $$\sqrt{3}x+y+2=0$$ we get, $$\sqrt{3}x+y=-2$$ Now, you can write the value of $\cos \theta =\sqrt{3}\And \sin \theta =1$ if you don’t know that “p” is the length of the perpendicular from the origin and we know that length cannot be negative. Also, if you don’t know the value of $\cos \theta \And \sin \theta $ lies from -1 to 1 then also you can write these values of $\cos \theta \And \sin \theta $ so make sure you won’t make such mistakes.