Question

Find the values of the other five trigonometric functions in $\cos \theta =-\dfrac{1}{2},\theta$ in quadrant II.

Answer 1

Hint:Draw a right angled triangle with the help of given expression $\cos \theta =-\dfrac{1}{2}$ by not considering the negative sign and using the relation $\cos \theta =\dfrac{base}{hypotenuse}$ find the unknown side of the right angled triangle with the help of Pythagoras theorem given as
${{\left( hypotenuse \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$
Sin, cosec are positive in the 2nd quadrant and other trigonometric functions are negative. $\sin \theta ,\tan \theta$ for a right angle.
$\sin \theta =\dfrac{perpendicular}{hypotenuse},\,\tan \theta =\dfrac{perpendicular}{base}$
And $\sec \theta ,\,\cos ec\theta ,\,\cot \theta$ are just opposite to $\cos \theta ,\,\sin \theta \,and\,\tan \theta$ respectively. Use the above identities to evaluate the values of other five functions.

Complete step-by-step answer:
We know the value of $\cos \theta$ from the problem as
$\cos =-\dfrac{1}{2}............(i)$
Where, $\theta$ is lying in the 2nd quadrant. Now we know any trigonometric function takes a negative or positive sign according to the quadrant of the angle inside the trigonometric function. But the definition of it will not change. Hence, as we know,
$\cos \theta =\dfrac{base}{hypotenuse}$
So, we can ignore the negative sign for drawing a right-angle triangle for $\cos =-\dfrac{1}{2}$ with the help of the above-mentioned formula.
So, let us draw a triangle for $\cos =\dfrac{1}{2}$, where 1 is base 2 is acting as hypotenuses of triangle. So, we get,

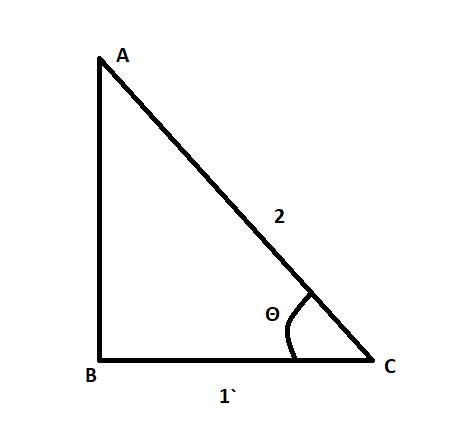
Now, we know the Pythagoras theorem relation in a right -triangle can be given as ${{\left( hypotenuse \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}............(iii)$
Now, we can get the equation (iii) by using the given triangle ABC as

& {{\left( AC \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}} \\\ & {{\left( 2 \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( 1 \right)}^{2}} \\\ & {{\left( AB \right)}^{2}}=4-1=3 \\\ & Ab=\sqrt{3} \\\ \end{aligned}$$ write here "Hence, ABC triangle can be drawn as"  Now, we know the value of $\cos \theta =-\dfrac{1}{2}$ and we have a triangle ABC which is defined according to the given function in the problem. So, let's relate other trigonometric functions with the help of property or rules of quadrants defined for trigonometric functions.  So, as per the given statement in the problem $\theta $ is lying in the IIrd quadrant, where sin and cosec are positive only and others will give negative value only. So, let us observe the triangle ABC and rules of quadrant for writing values of trigonometric functions. (i) $\sin \theta $ As we know $\sin \theta =\dfrac{perpendicular}{base}.............(iv)$ As we know sin function is positive in the 2nd quadrant. So, using$\vartriangle ABC$, we can write the value of $\sin \theta $ as $\dfrac{\sqrt{3}}{2}$ from the equation (iv) but need to put a negative sign as the angle belongs to the 2nd quadrant. Hence, we get $\sin \theta =\dfrac{\sqrt{3}}{2}$ (ii) $\cos \theta $ Similarly, as we know cos is also negative in the 2nd quadrant. So, $$\cos \theta =\dfrac{base}{hypothesis}.............(v)$$ From $\vartriangle ABC$ $\cos \theta =-\dfrac{1}{2}$ (iii) $$\tan \theta $$ $$\tan \theta =\dfrac{perpendicular}{base}$$ Tan is negative in the 2rd quadrant. So, we get $$\begin{aligned} & \tan \theta =-\dfrac{\sqrt{3}}{1} \\\ & \tan \theta =-\sqrt{3} \\\ \end{aligned}$$ (iv) $$\sec \theta $$ $$\sec \theta =\dfrac{hypotenuse}{base}$$ Sec is negative in the 2nd quadrant. So, we get $$\begin{aligned} & \sec \theta =-\dfrac{2}{1} \\\ & \sec \theta =-2 \\\ \end{aligned}$$ (v) $$co\sec \theta $$ $$co\sec \theta =\dfrac{hypotenuse}{perpendicular}$$ Cosec is also positive in the 2nd quadrant. So, we get $\cos ec\theta =\dfrac{2}{\sqrt{3}}$ (vi) $\cot \theta $ As we know $\sec \theta $ can be given as $$\cot \theta =\dfrac{perpendicular}{base}$$ As $\cot \theta $ is negative in 2nd quadrant, so, we get $\cot \dfrac{1}{\sqrt{3}}$ Hence, values of all the trigonometric functions is given as $\begin{aligned} & \sin \theta =\dfrac{\sqrt{3}}{2} \\\ & \cos \theta =-\dfrac{1}{2} \\\ & \tan \theta =-\sqrt{3} \\\ & \cot \theta =-\dfrac{1}{\sqrt{3}} \\\ & \cos ec\theta =\dfrac{2}{\sqrt{3}} \\\ & \sec \theta =-2 \\\ \end{aligned}$ Note: Do not confuse with the negative sign in the given expression i.e. $\cos \theta =-\dfrac{1}{2}$. It will not play any role for drawing the right angle triangle sign will be determined only by the quadrant, it means $\theta $ is lying in second quadrant, where cosine function Is negative, that’s why $\cos \theta $ is given as $-\dfrac{1}{2}$. So don’t confuse it with the negative sign. One may use, following identities to get other function as well: $\begin{aligned} & {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 \\\ & 1+{{\tan }^{2}}\theta =se{{c}^{2}}\theta \\\ & 1+{{\cot }^{2}}\theta =\cos e{{c}^{2}}\theta \\\ & \sin \theta =\dfrac{1}{\cos ec\theta } \\\ & \cos \theta =\dfrac{1}{\sec \theta } \\\ & \cot \theta =\dfrac{1}{\tan \theta }=\dfrac{\cos \theta }{\sin \theta } \\\ & \tan \theta =\dfrac{\sin \theta }{\cos \theta } \\\ \end{aligned}$ But need to take care of quadrant rules for the trigonometric function with the above identities as well. We can eliminate making a right-angle triangle step only with this approach.