Question

Find the values of the other five trigonometric functions if $\tan \theta =\dfrac{3}{4}$, $\theta$ in quadrant III.

Answer 1

Hint:First of all, try to recollect the signs of the various trigonometric ratios in the third quadrant. Now, find $\cot \theta$ by using $\dfrac{1}{\tan \theta }$, $\sec \theta$ by $\sqrt{1+{{\tan }^{2}}\theta }$, $\cos \theta$ by $\dfrac{1}{\sec \theta }$, $\sin \theta$ by $\tan \theta \cos \theta$ , and so on.

Complete step-by-step answer:
In this question, we have to find the values of the other five trigonometric functions if $\tan \theta =\dfrac{3}{4}$, $\theta$ in quadrant III. Before proceeding with this question, let us see the sign of different trigonometric ratios in different quadrants. We have 6 trigonometric ratios and that are $\sin \theta ,\cos \theta ,\tan \theta ,\cot \theta ,\operatorname{cosec}\theta$ and $\sec \theta$.
1. In the first quadrant, that is from 0 to ${{90}^{o}}$ or 0 to $\dfrac{\pi }{2}$, all the trigonometric ratios are positive.
2. In the second quadrant, that is from ${{90}^{o}}$ to ${{180}^{o}}$ or $\dfrac{\pi }{2}$ to $\pi$, only $\sin \theta$ and $\operatorname{cosec}\theta$ are positive.
3. In the third quadrant, that is from ${{180}^{o}}$ to ${{270}^{o}}$ or $\pi$ to $\dfrac{3\pi }{2}$, only $\tan \theta$ and $\cot \theta$ are positive.
4. In the fourth quadrant, that is from ${{270}^{o}}$ to ${{360}^{o}}$ or $\dfrac{3\pi }{2}$ to $2\pi$, only $\cos \theta$ and $\sec \theta$ are positive.
This cycle would repeat after ${{360}^{o}}$.

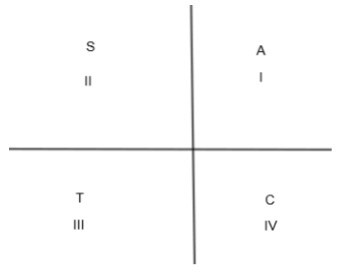
In this figure, A means all are positive, S means $\sin \theta$ and $\operatorname{cosec}\theta$ are positive, T means $\tan \theta$ and $\cot \theta$ are positive and C means $\cos \theta$ and $\sec \theta$ are positive.
Here, we are given that $\tan \theta =\dfrac{3}{4}$ and $\theta$ is in the third quadrant. So, here only $\tan \theta$ and $\cot \theta$ would be positive, and the remaining trigonometric ratios would be negative.
We know that $\cot \theta =\dfrac{1}{\tan \theta }$. By substituting the value of $\tan \theta =\dfrac{3}{4}$, we get,
$\cot \theta =\dfrac{1}{\dfrac{3}{4}}=\dfrac{4}{3}$
We know that, ${{\sec }^{2}}\theta =1+{{\tan }^{2}}\theta$. By substituting the value of $\tan \theta =\dfrac{3}{4}$, we get,
${{\sec }^{2}}\theta =1+{{\left( \dfrac{3}{4} \right)}^{2}}$
${{\sec }^{2}}\theta =1+\dfrac{9}{16}=\dfrac{25}{16}$
$\sec \theta =\sqrt{\dfrac{25}{16}}$
$\sec \theta =\pm \dfrac{5}{4}$
We know that $\sec \theta$ is negative in the third quadrant, so $\sec \theta =\dfrac{-5}{4}$.
We know that $\cos \theta =\dfrac{1}{\sec \theta }$, By substituting the value of $\sec \theta =\dfrac{-5}{4}$, we get,
$\cos \theta =\dfrac{1}{\dfrac{-5}{4}}$
$\cos \theta =\dfrac{-4}{5}$
We know that $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$
So, by substituting $\tan \theta =\dfrac{3}{4}$ and $\cos \theta =\dfrac{-4}{5}$, we get,
$\Rightarrow \dfrac{3}{4}=\dfrac{\sin \theta }{\left( \dfrac{-4}{5} \right)}$
x$\Rightarrow \dfrac{3}{4}=\sin \theta \times \dfrac{5}{-4}$
By multiplying $\left( \dfrac{-4}{5} \right)$ on both the sides of the above equation, we get,
$\left( \dfrac{-4}{5} \right).\left( \dfrac{3}{4} \right)=\sin \theta$
$\sin \theta =\dfrac{-3}{5}$
We know that $\operatorname{cosec}\theta =\dfrac{1}{\sin \theta }$
By substituting the value of $\sin \theta =\dfrac{-3}{5}$, we get,
$\operatorname{cosec}\theta =\dfrac{1}{\left( \dfrac{-3}{5} \right)}$
$\operatorname{cosec}\theta =\dfrac{-5}{3}$
So, if $\tan \theta =\dfrac{3}{4}$ and $\theta$ is in the third quadrant, the other 5 values we get as,
$\sin \theta =\dfrac{-3}{5}$
$\cos \theta =\dfrac{-4}{5}$
$\sec \theta =-\dfrac{5}{4}$
$\operatorname{cosec}\theta =\dfrac{-5}{3}$
$\cot \theta =\dfrac{4}{3}$

Note: In this question, we can also find the value of the magnitude of all the trigonometric ratios by considering a triangle according to the given information, that is $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}=\dfrac{3}{4}$ and writing other trigonometric ratios in terms of various sides of the triangle. Then we can later put the sign of the ratios according to the quadrant. Another method is after finding the angle $\cot \theta$, we can use the formula ${{\operatorname{cosec}}^{2}}\theta -{{\cot }^{2}}\theta =1$ to compute $\operatorname{cosec}\theta$ and then from this we can find $\sin \theta =\dfrac{1}{\operatorname{cosec}\theta }$.
.