Question

Find the values of the following trigonometric functions
(1) $\sin {75^ \circ }$
(2) $\cos ec( - {1410^ \circ })$
(3) $\tan \dfrac{{19\pi }}{3}$
(4) $\sin \left( {\dfrac{{ - 11\pi }}{3}} \right)$
(5) $\cot \left( {\dfrac{{ - 15\pi }}{4}} \right)$

Answer 1

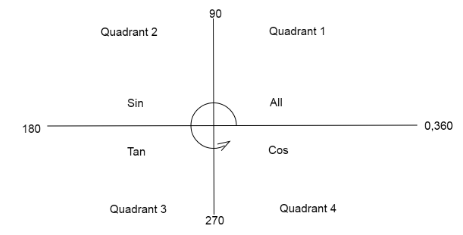
We will write each of the angles in each part in such a way that either we can apply some trigonometric formula on them or we can compare them using the quadrant diagram.
*$\sin (A + B) = \sin A\cos B + \cos A\sin B$

• We know the values of all trigonometric angles are positive in the first quadrant.
  Values of only $\sin \theta$ are positive in the second quadrant.
  Values of only $\tan \theta$ are positive in the third quadrant.
  Values of only $\cos \theta$ are positive in the fourth quadrant.
  

Complete step-by-step answer:
We will solve each part separately using trigonometric formulas and concepts.
(1) $\sin {75^ \circ }$
We can break the angle associated with the function into two parts and then use the formula of $\sin (A + B) = \sin A\cos B + \cos A\sin B$
We can write ${75^ \circ } = {45^ \circ } + {30^ \circ }$
$\Rightarrow \sin ({75^ \circ }) = \sin ({45^ \circ } + {30^ \circ })$
Apply formula $\sin (A + B) = \sin A\cos B + \cos A\sin B$
$\Rightarrow \sin ({75^ \circ }) = \sin ({45^ \circ })\cos ({30^ \circ }) + \cos ({45^ \circ })\sin ({30^ \circ })$
Now we substitute the value of $\sin ({45^ \circ }) = \dfrac{1}{{\sqrt 2 }};\cos ({45^ \circ }) = \dfrac{1}{{\sqrt 2 }};\cos ({30^ \circ }) = \dfrac{{\sqrt 3 }}{2};\sin ({30^ \circ }) = \dfrac{1}{{\sqrt 2 }}$
$\Rightarrow \sin ({75^ \circ }) = \left( {\dfrac{1}{{\sqrt 2 }} \times \dfrac{{\sqrt 3 }}{2}} \right) + \left( {\dfrac{1}{2} \times \dfrac{1}{{\sqrt 2 }}} \right)$
Multiply the values in RHS
$\Rightarrow \sin ({75^ \circ }) = \left( {\dfrac{{\sqrt 3 }}{{2\sqrt 2 }}} \right) + \left( {\dfrac{1}{{2\sqrt 2 }}} \right)$
Take LCM in RHS
$\Rightarrow \sin ({75^ \circ }) = \dfrac{{\sqrt 3 + 1}}{{2\sqrt 2 }}$
$\therefore$Value of $\sin ({75^ \circ })$ is $\dfrac{{\sqrt 3 + 1}}{{2\sqrt 2 }}$
(2) $\cos ec( - {1410^ \circ })$
We know sine function is an odd function, then cosecant function will also be an odd function.
$\Rightarrow \cos ec( - x) = - \cos ecx$
Here we can write
$\Rightarrow \cos ec( - {1410^ \circ }) = - \cos ec({1410^ \circ })$
Now we break the angle associated with cosine such that one part of it is multiple of any of the four values on the axis in quadrant diagram.
We can write ${1410^ \circ } = {1440^ \circ } - {30^ \circ }$
i.e. ${1440^ \circ } = 8 \times {180^ \circ } - {30^ \circ }$
Since we know that ${180^ \circ } = \pi$
$\Rightarrow {1440^ \circ } = 8 \times \pi - \dfrac{{30\pi }}{{180}}$
$\Rightarrow {1440^ \circ } = 8\pi - \dfrac{\pi }{6}$
$\Rightarrow \cos ec( - {1440^ \circ }) = - \cos ec(8\pi - \dfrac{\pi }{6})$
Now from the quadrant diagram, $8\pi$will be exactly where there are other even multiples of $\pi$.
If we subtract an angle from that point, we will get a value in the fourth quadrant, where only cosine values are positive and rest all values are negative.
$\Rightarrow \cos ec( - {1440^ \circ }) = - ( - \cos ec(\dfrac{\pi }{6}))$
Multiply both negative signs to obtain positive sign
$\Rightarrow \cos ec( - {1440^ \circ }) = \cos ec(\dfrac{\pi }{6})$
Since we know $\sin \dfrac{\pi }{6} = \dfrac{1}{2}$, then $\cos ec\dfrac{\pi }{6} = \dfrac{1}{{\dfrac{1}{2}}} = 2$
$\Rightarrow \cos ec( - {1440^ \circ }) = 2$
$\therefore$The value of $\cos ec( - {1440^ \circ })$ is 2.
(3) $\tan \dfrac{{19\pi }}{3}$
We can write $\dfrac{{19\pi }}{3} = \dfrac{{18\pi }}{3} + \dfrac{\pi }{3}$
$\tan \left( {\dfrac{{19\pi }}{3}} \right) = \tan \left( {\dfrac{{18\pi }}{3} + \dfrac{\pi }{3}} \right)$
Cancel same factors from numerator and denominator in angle
$\Rightarrow \tan \left( {\dfrac{{19\pi }}{3}} \right) = \tan \left( {6\pi + \dfrac{\pi }{3}} \right)$
From the quadrant diagram, $6\pi$ will be exactly where there are other even multiples of $\pi$.
If we add an angle from that point, we will get a value in the first quadrant, where all values are positive.
$\Rightarrow \tan \left( {\dfrac{{19\pi }}{3}} \right) = \tan \left( {\dfrac{\pi }{3}} \right)$
We know the value of $\tan \left( {\dfrac{\pi }{3}} \right) = \sqrt 3$
$\Rightarrow \tan \left( {\dfrac{{19\pi }}{3}} \right) = \sqrt 3$
$\therefore$The value of $\tan \left( {\dfrac{{19\pi }}{3}} \right)$ is $\sqrt 3$
(4) $\sin \left( {\dfrac{{ - 11\pi }}{3}} \right)$
We know sine function is an odd function,
$\Rightarrow \sin ( - x) = - \sin x$
Here we can write
$\Rightarrow \sin \left( {\dfrac{{ - 11\pi }}{3}} \right) = - \sin \left( {\dfrac{{11\pi }}{3}} \right)$
Now we can write $\dfrac{{11\pi }}{3} = \dfrac{{12\pi }}{3} - \dfrac{\pi }{3}$
$\Rightarrow \sin \left( {\dfrac{{ - 11\pi }}{3}} \right) = - \sin \left( {\dfrac{{12\pi }}{3} - \dfrac{\pi }{3}} \right)$
Cancel same factors from numerator and denominator in angle
$\Rightarrow \sin \left( {\dfrac{{ - 11\pi }}{3}} \right) = - \sin \left( {4\pi - \dfrac{\pi }{3}} \right)$
From the quadrant diagram, $4\pi$ will be exactly where there are other even multiples of $\pi$.
If we subtract an angle from that point, we will get a value in the fourth quadrant, where only cosine values are positive, rest all values are negative.
$\Rightarrow \sin \left( {\dfrac{{ - 11\pi }}{3}} \right) = - \left( { - \sin \left( {\dfrac{\pi }{3}} \right)} \right)$
Multiply both negative signs to make positive sign
$\Rightarrow \sin \left( {\dfrac{{ - 11\pi }}{3}} \right) = \sin \left( {\dfrac{\pi }{3}} \right)$
We know the value of $\sin \dfrac{\pi }{3} = \dfrac{1}{2}$
$\Rightarrow \sin \left( {\dfrac{{ - 11\pi }}{3}} \right) = \dfrac{1}{2}$
$\therefore$The value of $\Rightarrow \sin \left( {\dfrac{{ - 11\pi }}{3}} \right)$ is $\dfrac{1}{2}$
(5) $\cot \left( {\dfrac{{ - 15\pi }}{4}} \right)$
Since cotangent is an odd function
$\Rightarrow \cot ( - x) = - \cot x$
$\Rightarrow \cot \left( {\dfrac{{ - 15\pi }}{4}} \right) = - \cot \left( {\dfrac{{15\pi }}{4}} \right)$
Now we can write $\dfrac{{15\pi }}{4} = \dfrac{{16\pi }}{4} - \dfrac{\pi }{4}$
$\Rightarrow \cot \left( {\dfrac{{ - 15\pi }}{4}} \right) = - \cot \left( {\dfrac{{16\pi }}{4} - \dfrac{\pi }{4}} \right)$
Cancel same factors from numerator and denominator in angle
$\Rightarrow \cot \left( {\dfrac{{ - 15\pi }}{4}} \right) = - \cot \left( {4\pi - \dfrac{\pi }{4}} \right)$
From the quadrant diagram, $4\pi$will be exactly where there are other even multiples of $\pi$.
If we subtract an angle from that point, we will get a value in the fourth quadrant, where only cosine values are positive, rest all values are negative.
$\Rightarrow \cot \left( {\dfrac{{ - 15\pi }}{4}} \right) = - \left( { - \cot \left( {\dfrac{\pi }{4}} \right)} \right)$
Multiply both negative signs to make positive sign
$\Rightarrow \cot \left( {\dfrac{{ - 15\pi }}{4}} \right) = \cot \left( {\dfrac{\pi }{4}} \right)$
Since we know the value of $\tan \left( {\dfrac{\pi }{4}} \right) = 1 \Rightarrow \cot \left( {\dfrac{\pi }{4}} \right) = 1$
$\Rightarrow \cot \left( {\dfrac{{ - 15\pi }}{4}} \right) = 1$
$\therefore$The value of $\cot \left( {\dfrac{{ - 15\pi }}{4}} \right)$ is 1.

Note: Students are likely to make mistakes while calculating the values from the quadrant diagram, keep in mind that we always move anti-clockwise as we add the angles, so when we subtract the angle we move backwards or clockwise to see which quadrant our function lies in.
Students can take the help of table which gives us the values of some trigonometric functions at common angles like ${0^ \circ },{30^ \circ },{45^ \circ },{60^ \circ },{90^ \circ }$ is

ANGLEFUNCTION	${0^ \circ }$	${30^ \circ }$	${45^ \circ }$	${60^ \circ }$	${90^ \circ }$
Sin	0	$\dfrac{1}{2}$	$\dfrac{1}{{\sqrt 2 }}$	$\dfrac{{\sqrt 3 }}{2}$	1
Cos	1	$\dfrac{{\sqrt 3 }}{2}$	$\dfrac{1}{{\sqrt 2 }}$	$\dfrac{1}{2}$	0
Tan	0	$\dfrac{1}{{\sqrt 3 }}$	1	$\sqrt 3$	Not defined