Question

Find the values of $\cos ec\left( {{{60}^ \circ }} \right)$, $\sec \left( {{{60}^ \circ }} \right)$ and $\cot \left( {{{60}^ \circ }} \right)$.

Answer 1

The given question involves the basic concepts of trigonometric functions. The value of trigonometric ratios is always calculated in a right angled triangle. There are six main trigonometric ratios which are the ratios of different pairs of sides of a right angled triangle: base, altitude and hypotenuse. We first draw a right angled triangle and then calculate the trigonometric ratios accordingly.

Complete step by step answer:
The trigonometry is a Greek word whose meaning is derived as: “Tri” means three while “Gon” means sides and “Metron” means measure. It helps in studying the relation between the three sides and three angles of the triangle. The main values at which trigonometric ratios are given and easy to calculate area: ${0^ \circ }$, ${30^ \circ }$, ${45^ \circ }$, ${60^ \circ }$ and ${90^ \circ }$. The values of the six trigonometric ratios is easy to determine at multiples of the above given numbers.

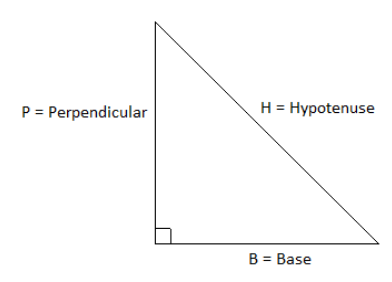
Trigonometric ratios in terms of sides of triangle are given as:
Sine of an angle is the ratio of perpendicular side to the angle to the hypotenuse of the triangle. So, $\sin \theta = \dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. Cosine of an angle is the ratio of the base side of the angle to the hypotenuse of the triangle. So, $\cos \theta = \dfrac{\text{Base}}{\text{Hypotenuse}}$.

Tangent of an angle is the ratio of perpendicular side to the angle to the base side of the angle. So, $\tan \theta = \dfrac{\text{Perpendicular}}{\text{Base}}$. Now, cotangent, cosecant and secant are the reciprocal functions of tangent, sine and cosine functions respectively. So, we get, Cosecant of an angle is the ratio of hypotenuse of the triangle to the perpendicular side to the angle. So,
$\cos ec\theta = \dfrac{\text{Hypotenuse}}{\text{Perpendicular}}$.

Secant of an angle is the ratio of hypotenuse of the triangle to the base side of the angle. So, $\sec \theta = \dfrac{\text{Hypotenuse}}{\text{Base}}$.
Cotangent of an angle is the ratio of base side of angle to the perpendicular side to the angle.
The values of trigonometric ratios for angle ${60^ \circ }$ are given as:
$\cos ec\left( {{{60}^ \circ }} \right) = \dfrac{2}{{\sqrt 3 }}$
$\Rightarrow \sec \left( {{{60}^ \circ }} \right) = \dfrac{1}{2}$
$\therefore \cot \left( {{{60}^ \circ }} \right) = \dfrac{1}{{\sqrt 3 }}$

Note: The value of trigonometric ratio of given angle remains the same and does not change according to change in sides of the triangle as the ratio of the sides of the triangle remains same. We must know the values of trigonometric functions for some standard angles in order to solve the given question.