Question

Find the values and then prove the expression ${{\cos }^{-1}}\left( \dfrac{12}{13} \right)+{{\sin }^{-1}}\left( \dfrac{3}{5} \right)={{\sin }^{-1}}\left( \dfrac{56}{65} \right)$

Answer 1

Hint: We will apply the trigonometric formula $\cos \left( \theta \right)=\dfrac{\text{Base}}{\text{Hypotenuse}}$ and $\sin \left( a \right)=\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$ to prove the expression. Also, we will use Pythagoras theorem here.

Complete step-by-step answer:
${{\cos }^{-1}}\left( \dfrac{12}{13} \right)+{{\sin }^{-1}}\left( \dfrac{3}{5} \right)={{\sin }^{-1}}\left( \dfrac{56}{65} \right)$
$\begin{aligned} & {{\cos }^{-1}}\left( \dfrac{12}{13} \right)=a \\\ & \Rightarrow \left( \dfrac{12}{13} \right)=\cos \left( a \right) \\\ \end{aligned}$
Since, we know that $\cos \left( \theta \right)=\dfrac{\text{Base}}{\text{Hypotenuse}}$. Therefore we can have 12 as a base and 13 as a hypotenuse of a right angled triangle as shown below. Therefore, we have

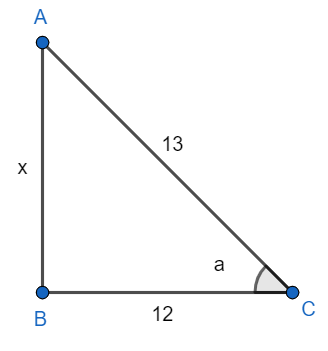
So, by Pythagoras theorem we have
$\begin{aligned} & {{\left( 13 \right)}^{2}}={{\left( 12 \right)}^{2}}+{{x}^{2}} \\\ & \Rightarrow {{\left( 13 \right)}^{2}}-{{\left( 12 \right)}^{2}}={{x}^{2}} \\\ & \Rightarrow 169-144={{x}^{2}} \\\ & \Rightarrow {{x}^{2}}=25 \\\ & \Rightarrow x=5 \\\ \end{aligned}$
Now this x = 5 is the value of perpendicular. Therefore, we can find the value of $\sin \left( a \right)=\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. Since, perpendicular is 5 units and hypotenuse is 13. Therefore, we have $\sin \left( a \right)=\dfrac{5}{13}$.
Now we will consider ${{\sin }^{-1}}\left( \dfrac{3}{5} \right)=b$. By taking the inverse sine operator to the right side of the equation we have $\left( \dfrac{3}{5} \right)=\sin \left( b \right)$. Since, we know that $\sin \left( a \right)=\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. Therefore we can have 3 as perpendicular and 5 as a hypotenuse of a right angled triangle as shown below. Therefore, we have

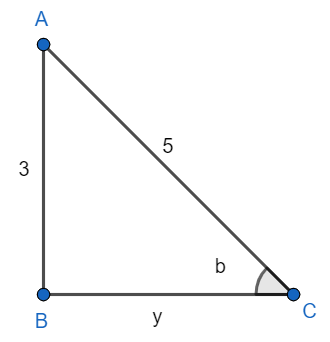
So, by Pythagoras theorem we have
$\begin{aligned} & {{\left( 5 \right)}^{2}}={{\left( 3 \right)}^{2}}+{{y}^{2}} \\\ & \Rightarrow {{\left( 5 \right)}^{2}}-{{\left( 3 \right)}^{2}}={{y}^{2}} \\\ & \Rightarrow {{y}^{2}}=25-9 \\\ & \Rightarrow {{y}^{2}}=16 \\\ & \Rightarrow y=\pm 4 \\\ \end{aligned}$
Since the side cannot be negative therefore we have y = 4. Now this side BC will work as a base of the triangle. Thus, we can find the value of $\cos \left( b \right)=\dfrac{\text{Base}}{\text{Hypotenuse}}$. Since, the base is now 4 units and the hypotenuse is 5 units therefore we get $\cos \left( b \right)=\dfrac{4}{5}$.
Now we will apply the formula $\sin \left( a+b \right)=\sin \left( a \right)\cos \left( b \right)+\cos \left( a \right)\sin \left( b \right)$. Now by substituting the values in this formula we have
$\begin{aligned} & \sin \left( a+b \right)=\dfrac{5}{13}\times \dfrac{4}{5}+\dfrac{12}{13}\times \dfrac{3}{5} \\\ & \Rightarrow \sin \left( a+b \right)=\dfrac{20}{65}+\dfrac{36}{65} \\\ & \Rightarrow \sin \left( a+b \right)=\dfrac{56}{65} \\\ \end{aligned}$
Now we will take the sine operation to the right side of the equation. Therefore, we get $\begin{aligned} & \sin \left( a+b \right)=\dfrac{56}{65} \\\ & \Rightarrow a+b={{\sin }^{-1}}\left( \dfrac{56}{65} \right) \\\ \end{aligned}$
As we know that the values of a and b are given as ${{\cos }^{-1}}\left( \dfrac{12}{13} \right)=a$ and ${{\sin }^{-1}}\left( \dfrac{3}{5} \right)=b$. Therefore, by substituting the values in the expression $a+b={{\sin }^{-1}}\left( \dfrac{56}{65} \right)$. Therefore we get ${{\cos }^{-1}}\left( \dfrac{12}{13} \right)+{{\sin }^{-1}}\left( \dfrac{3}{5} \right)={{\sin }^{-1}}\left( \dfrac{56}{65} \right)$.
Hence, the expression ${{\cos }^{-1}}\left( \dfrac{12}{13} \right)+{{\sin }^{-1}}\left( \dfrac{3}{5} \right)={{\sin }^{-1}}\left( \dfrac{56}{65} \right)$ is proved.

Note: We could have solved it by an alternate method. In this method we can solve it as $\begin{aligned} & {{\cos }^{-1}}\left( \dfrac{12}{13} \right)=a \\\ & \Rightarrow \left( \dfrac{12}{13} \right)=\cos \left( a \right) \\\ \end{aligned}$
By using the trigonometry identity here which is given by ${{\cos }^{2}}\left( a \right)+{{\sin }^{2}}\left( a \right)=1$. This results in ${{\sin }^{2}}\left( a \right)=1-{{\cos }^{2}}\left( a \right)$. Therefore we have
$\begin{aligned} & {{\sin }^{2}}\left( a \right)=1-{{\cos }^{2}}\left( a \right) \\\ & \Rightarrow {{\sin }^{2}}\left( a \right)=1-{{\left( \dfrac{12}{13} \right)}^{2}} \\\ & \Rightarrow {{\sin }^{2}}\left( a \right)=1-\dfrac{144}{169} \\\ & \Rightarrow {{\sin }^{2}}\left( a \right)=\dfrac{169-144}{169} \\\ & \Rightarrow {{\sin }^{2}}\left( a \right)=\dfrac{25}{169} \\\ & \Rightarrow \sin \left( a \right)=\dfrac{5}{13} \\\ \end{aligned}$
Similarly, we can solve the remaining by this formula and get the desired proof.