Question

Find the value(s) of x for which
$y = {\left[ {x\left( {x - 2} \right)} \right]^2}$
is an increasing function.

Answer 1

Hint : To find the points or intervals where the given function is increasing, we need to follow the procedure:
Calculate $\dfrac{{dy}}{{dx}}$ , equate it equal to zero to get the values of a.
The intervals where $\dfrac{{dy}}{{dx}} > 0$ , at these the function is increasing.
Apply:
$\dfrac{{d\left( {uv} \right)}}{{dx}} = u\dfrac{{dv}}{{dx}} + v\dfrac{{du}}{{dx}}$

Complete step-by-step answer :
We have,
$y = {\left[ {x\left( {x - 2} \right)} \right]^2}$

Differentiating to the sides w.r.t x, we get
$\dfrac{{dy}}{{dx}} = 2[x(x - 2)]\dfrac{d}{{dx}}[x(x - 2)]$
$\left[ {{\text{Because }}\dfrac{d}{{dx}}({x^n}) = n{x^{n - 1}}\dfrac{d}{{dx}}(x)} \right]$
$= 2({x^2} - 2x).(2x - 2)$
[Simplifying]
$\dfrac{{dy}}{{dx}} = 4x\left( {x - 1} \right)\left( {x - 2} \right)$ ------(1)
Equating this to zero, we obtain:
$\dfrac{{dy}}{{dx}} = 0$
$4x\left( {x - 1} \right)\left( {x - 2} \right) = 0$
The values of x are:
X=0, x=1 and x=2
Intervals can be written as:
$\left( { - \infty ,0} \right),\left( {0,1} \right)\left( {1,2} \right),\left( {2,\infty } \right)$

Checking the points on the number line by substituting these in (1), we get:

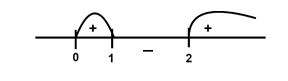
$\dfrac{{dy}}{{dx}}$ for intervals the value of x is:
(0,1) is positive
(1,2) is negative
(2,∞ is positive
Therefore, it can be said that the given function is increasing in the intervals
$x \in \left( {0,1} \right) \cup \left( {2,\infty } \right)$

Note : Always check on number line the substituted values of x in $\dfrac{{dy}}{{dx}}$ so as to confirm the interval where function increases/decreases