Question
Question: Find the value of λ, where [.] denotes the greatest integer function, and λ = $\left[\frac{10(\sqrt...
Find the value of λ, where [.] denotes the greatest integer function, and
λ = [(27+0+27−1+27−2+27−3+...+27−729)10(27+0+27+1+27+2+27+3+...+27+729)]
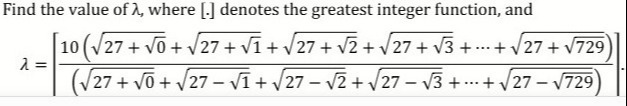
Answer
-19
Explanation
Solution
- Let the expression be DN.
- The numerator part is N=10∑k=0729(27+k)=10(73027+∑k=0729k).
- The denominator part is D=(27+0)+∑k=1729(27−k)=73027−∑k=1729k.
- Let A=73027 and Y=∑k=1729k. Note ∑k=0729k=Y.
- The expression becomes A−Y10(A+Y).
- We approximate Y≈∫0729xdx=32(7293/2)=13122.
- A=73027=21903≈3793.
- Since Y>A, A−Y is negative.
- The fraction is approximately 3793−1312210(3793+13122)=−932910(16915)≈−18.13.
- Therefore, λ=[−18.13]=−19.
