Question
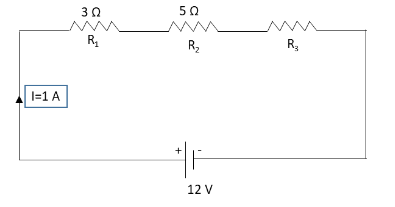
Question: Find the value of unknown resistance \[{R_3}\] in the above circuit using Kirchhoff’s voltage law. ...
Find the value of unknown resistance R3 in the above circuit using Kirchhoff’s voltage law.
Solution
Recall the basics of the Kirchhoff’s voltage law. Check how to apply Kirchhoff’s voltage law to a loop. Consider the loop given in the circuit diagram in question and apply Kirchhoff’s voltage law to this loop. Solve the equation obtained from the law and determine the value of the unknown resistance R3.
Complete step by step answer:
We have given a circuit diagram consisting of three resistances R1, R2 and R3. The value of the resistance R1 is 3Ω and the value of resistance R2 is 5Ω. The current flowing in the given circuit is 1A.
I=1A
We have asked to determine the value of the resistance R3 using Kirchhoff’s voltage law. Consider the given circuit diagram as the loop of the circuit. Apply Kirchhoff’s voltage law to this loop to determine the value of unknown resistance R3 in the loop.
−(12V)+IR1+IR2+IR3=0
⇒−(12V)+I(R1+R2+R3)=0
Substitute 1A for I, 3Ω for R1 and 5Ω for R2 in the above equation.
⇒−(12V)+(1A)(3Ω+5Ω+R3)=0
⇒−12+8+R3=0
⇒−4+R3=0
∴R3=4Ω
Hence, the value of the unknown resistance R3 using Kirchhoff’s voltage law is 4Ω.
Additional information:
Kirchhoff's voltage law states that the sum of all the potentials in a loop including emf’s and the resistances of the resistors in the given circuit diagram is equal to zero. This is also known as Kirchhoff’s second law or loop rule. There is another law stated by Kirchhoff’s known as Kirchhoff’s current law. This law states that the total current going into a junction is equal to the total current coming out of the junction.
Note: The students should be careful while applying Kirchhoff’s voltage law to the considered loop in the circuit diagram because if this law is not applied correctly with the correct signs of the potentials then the final value of the unknown resistance in the circuit will also be incorrect.
