Question

Find the value of trigonometric expression $\sin {{510}^{\circ }}$ .

Answer 1

Hint:Sin function is positive in 1st and 2nd quadrant and negative in 3rd and 4th quadrant. And if the angle inside the trigonometric function is of type $\dfrac{n\pi }{2}\pm \theta$ (where n is an odd), then change sin to cos, otherwise, if angle of type $n\pi \pm \theta$ , then do not change the trigonometric function, use these rules to solve the given problem. Use the value of $\sin \left( \dfrac{\pi }{6} \right)=\left( \dfrac{1}{2} \right)$ .

Complete step-by-step answer:
Here, we have to determine the value of the trigonometric term $\sin {{510}^{\circ }}$ .
So, let us suppose the value of the given trigonometric expression in the problem ‘P’.
Hence, we can write equation as –
$p=\sin {{510}^{\circ }}$ ……………………. (i)
Now, we can observe that the angle involved in the above expression is not lying in $0{}^\circ$ to ${{90}^{\circ }}$. It means we have to convert the given angle to acute angle form with the help of some trigonometric identities.
Hence, Let us divide the given expression by ${{180}^{\circ }}$ . So, that we can write the given angle in form of sum of angle which is multiple of ${{180}^{\circ }}$in following way:-
$510{}^\circ =180\times 3-{{30}^{\circ }}$ ……………………….. (ii)
Now, as we know the radian representation of $180{}^\circ$ is given as –
$\pi$radian $=180{}^\circ$ ………………… (iii)
$30{}^\circ$ in radian from the above expression as –
$30{}^\circ =\dfrac{\pi }{6}$ ………………………….. (iv)
Hence, we can re-write the expression (ii) with the help of equation (iii) and (iv) .
Now, we can put the angle $510{}^\circ$ as $3\pi -\dfrac{\pi }{6}$ to the equation (i). So, we get –
$510{}^\circ =3\pi -\dfrac{\pi }{6}$ ………………………… (v)
Now, as we know the quadrant angles are defined as

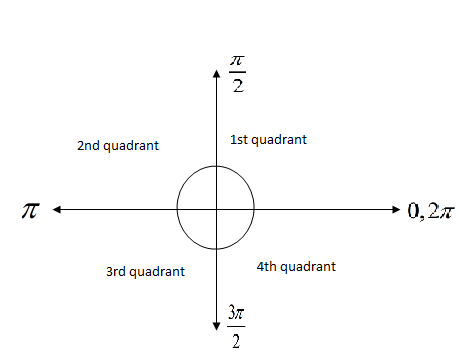
Now, we can apply the trigonometric rules for conversion of trigonometric expression by changing its angle.
$p=\sin \left( 3\pi -\dfrac{\pi }{6} \right)$ ……………………………………….. (vi)
Now, we can observe that the angle $3\pi -\dfrac{\pi }{6}$ will lie in 2nd quadrant because angle $3\pi$ will lie at the same position where $\pi$ is lying if we rotate ${{360}^{\circ }}$ or $2\pi$ from the position $\pi$, and we are subtracting $\dfrac{\pi }{6}$ from $3\pi$ , it means the result will lie in 2nd quadrant.
Now, as the angle is lying in the second quadrant and we know very well, sine function is positive in the second quadrant. So, conversion of sine by changing angle will not affect the sign of resultant. And as the angle $3\pi -\dfrac{\pi }{6}$ is written by involvement of angle $3\pi$ which is a multiple of ‘$\pi$’, it means the trigonometric function will remain same as per the rules of conversion of trigonometric functions by hanging their angles.
Hence, we can write identities related to above concept as –
$\begin{aligned} & \sin \left( \pi -\theta \right)=\sin \theta \\\ & \sin \left( 3\pi -\theta \right)=\sin \theta \\\ & \sin \left( 5\pi -\theta \right)=\sin \theta \\\ \end{aligned}$
. . .
. . .
. . .
$\sin \left( n\pi -\theta \right)=\sin \theta$ ………… (vii)
Where n is an odd integer.
Hence, using equation (vii) , we can write equation (vi) as
$p=\sin \left( 3\pi -\dfrac{\pi }{6} \right)=\sin \dfrac{\pi }{6}$
Now, we know the value of $\sin \dfrac{\pi }{6}$ is given as $\dfrac{1}{2}$ . So, we get the value of P as –
$p=\sin \dfrac{\pi }{6}=\dfrac{1}{2}$ .
Hence, the value of the given expression in the problem is $\dfrac{1}{2}$ .
$\sin 510{}^\circ =\dfrac{1}{2}$ .

Note: We need to know two important rules involved for conversion of trigonometric function with respect to the angles.
(i) Take care of the sign with the help of the given trigonometric function and the quadrant in which the angle is lying. This rule can be given as.
(ii) If the angle involved inside trigonometric function is multiply of $\dfrac{\pi }{2}$ (not multiple of $\pi$) i.e. $\dfrac{n\pi }{2}\pm \theta$ type, where n is an odd integer, then we need to convert the
$\begin{aligned} & \sin \rightleftarrows \cos \\\ & \tan \rightleftarrows \cot \\\ & \sec \rightleftarrows \cos ec \\\ \end{aligned}$
And if the angle involved in the sum is multiple of $\pi$ i.e. $n\pi \pm \theta$ type, then the trigonometric function will remain the same.
Don’t go for calculating the exact value directly with any other identity, it will be a complex approach and may give wrong answers as well. So, always try to solve these kinds of questions by the way given in solution.