Question

Find the value of trigonometric expression $\dfrac{\cos {{22}^{\circ }}}{\sin {{68}^{\circ }}}$.

Answer 1

Select either cosine function or sine function in the numerator or denominator respectively of the given expression and apply the complementary angle conversion formula as $\cos \left( {{90}^{\circ }}-\theta \right)=\sin \theta$ or $\sin \left( {{90}^{\circ }}-\theta \right)=\cos \theta$. If cosine function is selected then use the first formula and if sine function is selected then use the second formula. Cancel the like terms and get the answer.

Complete step-by-step solution:
Here, we have been provided with the trigonometric expression, $\dfrac{\cos {{22}^{\circ }}}{\sin {{68}^{\circ }}}$ and we have to find its value. Let us assume its value as ‘t’.
$\Rightarrow t=\dfrac{\cos {{22}^{\circ }}}{\sin {{68}^{\circ }}}$
Here, we are going to use the complementary angle conversion formula to simplify the expression. But first, let us see what is the meaning of complementary angles and how its rule is implemented.
Now, complementary angles are the pairs of angles whose sum equals 90 degrees. For example, ${{30}^{\circ }}\text{ and }{{60}^{\circ }},{{45}^{\circ }}\text{ and }{{45}^{\circ }},{{70}^{\circ }}\text{ and }{{20}^{\circ }}$ are some pairs of complementary angles.
Now, let us assume a right-angled triangle ABC.

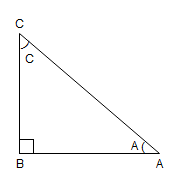
In the above figure, the triangle is right angled at B and A and C are acute angles. We know that.
$\begin{aligned} & \angle A+\angle B+\angle C={{180}^{\circ }} \\\ & \Rightarrow \angle A+{{90}^{\circ }}+\angle C={{180}^{\circ }} \\\ & \Rightarrow \angle A+\angle C={{90}^{\circ }} \\\ & \Rightarrow \angle A={{90}^{\circ }}-\angle C\ldots \ldots \ldots \left( i \right) \\\ \end{aligned}$
Now, we know that sine of an angle is the ratio of the perpendicular to the hypotenuse and cosine of an angle is the ratio of base to the hypotenuse of a right angled triangle. So, we have
$\begin{aligned} & \sin A=\dfrac{BC}{AC}\text{ and }\cos C=\dfrac{BC}{AC} \\\ & \Rightarrow \sin A=\cos C \\\ \end{aligned}$
Using relation (i), we get
$\Rightarrow \sin \left( {{90}^{\circ }}-C \right)=\cos C$
Similarly, we can prove that $\sin C=\cos \left( {{90}^{\circ }}-\theta \right)$ . Therefore, the conclusion is if $\theta$ is an acute angle, then $\cos \left( {{90}^{\circ }}-\theta \right)=\sin \theta$ and $\sin \left( {{90}^{\circ }}-\theta \right)=\cos \theta$.
Now, let us come to the question. Here, let us change the numerator of the given expression from cosine to sine function. So, we have
$\begin{aligned} & \Rightarrow E=\dfrac{\sin \left( {{90}^{\circ }}-{{22}^{\circ }} \right)}{\sin {{68}^{\circ }}} \\\ & \Rightarrow E=\dfrac{\sin {{68}^{\circ }}}{\sin {{68}^{\circ }}} \\\ & \Rightarrow E=1 \\\ \end{aligned}$
Hence, the value of the given expression is 1.

Note: One must remember the formulas of complementary angle conversion rules for all the six trigonometric functions because they are not derived everywhere but directly used. You may note that we have converted the numerator from cosine to sine. You may also convert the denominator from sine to cosine. But remember that we have to convert one of them and not both at the same time.