Question

Find the value of the given trigonometric ratio, $\tan 15{}^\circ$ .

Answer 1

Hint: Use the formula of $\tan 2A$ along with the value of $\tan 30{}^\circ$ , to get a quadratic equation. Solve the quadratic equation to reach the required answer.

Complete step-by-step answer:
We know;
$\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$

The other commonly used trigonometric values include:
$\tan 0{}^\circ =0$
$\tan 45{}^\circ =1$
$\tan 60{}^\circ =\sqrt{3}$

Also, we have, the formula: $\tan 2A=\dfrac{2\tan A}{1-{{\tan }^{2}}A}$

So, in the above formula substituting $A=15{}^\circ$ .
$\therefore \tan 2A=\dfrac{2\tan A}{1-{{\tan }^{2}}A}$
$\Rightarrow \tan \left( 2\times 15{}^\circ \right)=\dfrac{2\tan 15{}^\circ }{1-{{\tan }^{2}}15{}^\circ }$
$\Rightarrow \tan 30{}^\circ =\dfrac{2\tan 15{}^\circ }{1-{{\tan }^{2}}15{}^\circ }$

Putting the value of $\tan 30{}^\circ$ in the equation, we get;
$\dfrac{1}{\sqrt{3}}=\dfrac{2\tan 15{}^\circ }{1-{{\tan }^{2}}15{}^\circ }$

On cross-multiplication, we get;
$1-{{\tan }^{2}}15{}^\circ =2\sqrt{3}\tan 15{}^\circ$
$\Rightarrow {{\tan }^{2}}15{}^\circ +2\sqrt{3}\tan 15{}^\circ -1=0$

So, the equation we get is a quadratic equation, and one of the roots of this quadratic equation would be the value of $\tan 15{}^\circ$.

We know, for a quadratic equation of the form $a{{x}^{2}}+bx+c=0$ .
$x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$

Applying the formula to our quadratic equation, we have;
$\tan 15{}^\circ =\dfrac{-2\sqrt{3}\pm \sqrt{{{\left( 2\sqrt{3} \right)}^{2}}-4\times 1\times \left( -1 \right)}}{2\times 1}$
$\Rightarrow \tan 15{}^\circ =\dfrac{-2\sqrt{3}\pm \sqrt{12+4}}{2}$
$\Rightarrow \tan 15{}^\circ =\dfrac{-2\sqrt{3}\pm \sqrt{16}}{2}$
$\Rightarrow \tan 15{}^\circ =\dfrac{-2\sqrt{3}\pm 4}{2}$

We know, $15{}^\circ$ lies in the first quadrant.

According to the graph of $\tan (x)$ :

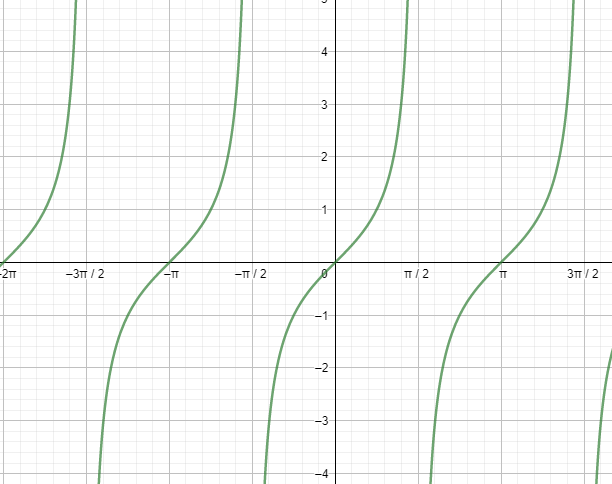
$\tan (x)$ is positive when x lies in the first quadrant.

Therefore, $\tan 15{}^\circ$ is also positive.
$\therefore \tan 15{}^\circ =\dfrac{-2\sqrt{3}+4}{2}$
$\Rightarrow \tan 15{}^\circ =\dfrac{\left( -\sqrt{3}+2 \right)}{{}}$
$\therefore \tan 15{}^\circ =2-\sqrt{3}$

Hence, the value of $\tan 15{}^\circ$ is $2-\sqrt{3}$ .

Note: Other useful formulas include:
$\tan (A+B)=\dfrac{\tan A+\tan B}{1-\tan A\tan B}$
$\tan (A-B)=\dfrac{\tan A-\tan B}{1+\tan A\tan B}$

And you are free to use any formula, just substitute the angles according to the need to get the desired values.

We can also find the value of $\tan 15{}^\circ$ using formula: $\tan (A-B)=\dfrac{\tan A-\tan B}{1+\tan A\tan B}$ .

On Substituting A and B in the above formula, we get;
$A=45{}^\circ$
$B=30{}^\circ$

The equation becomes:
$\tan (A-B)=\dfrac{\tan A-\tan B}{1+\tan A\tan B}$
$\Rightarrow \tan (45{}^\circ -30{}^\circ )=\dfrac{\tan 45{}^\circ -\tan 30{}^\circ }{1+\tan 45{}^\circ \tan 30{}^\circ }$
$\Rightarrow \tan 15{}^\circ =\dfrac{1-\left( \dfrac{1}{\sqrt{3}} \right)}{1+1\times \dfrac{1}{\sqrt{3}}}$

Point to remember: whenever you try to find the value of $\sin 15{}^\circ$ , don’t use the formula of $\sin 2A$ , instead, go for the formula: $\cos 2A=1-2{{\sin }^{2}}A$ . The reason being, whenever you use the formula of $\sin 2A$ , you get both $\cos A$ and $\sin A$ to be unknown, making it difficult to solve.