Solveeit Logo
Login

Question

Question: Find the value of the following trigonometric equation. \[\sin 120^\circ \times \cos 150^\circ - ...

Find the value of the following trigonometric equation.
sin⁡120∘×cos⁡150∘−cos⁡240∘×sin⁡330∘\sin 120^\circ \times \cos 150^\circ - \cos 240^\circ \times \sin 330^\circ
A. 1
B. -1
C. 23\dfrac{2}{3}
D. −(3+14) - \left( {\dfrac{{\sqrt 3 + 1}}{4}} \right)

Explanation

Solution

We had to use the trigonometric concept of different quadrant which states that all trigonometric values are positive in first quadrant, Sine and cosecant are positive in second quadrant, Tangent and cotangent are positive in third quadrant and cosine and secant are positive in fourth quadrant.

Complete step-by-step answer:

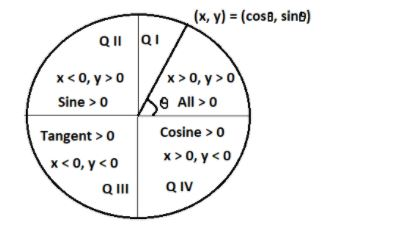
As we know that the above figure depicts how to transform one trigonometric function to another with proper sign convention.
As we see from the above figure that value of each trigonometric function is positive if θ\theta is in first quadrant (i.e. 0∘⩽θ⩽90∘0^\circ \leqslant \theta \leqslant 90^\circ )
Value of sin⁡θ\sin \theta and cos⁡ecθ\cos ec\theta is positive if (90∘⩽θ⩽180∘90^\circ \leqslant \theta \leqslant 180^\circ ). And all other trigonometric functions are negative.
Value of tan⁡θ\tan \theta and cot⁡θ\cot \theta is positive if (180∘⩽θ⩽270∘180^\circ \leqslant \theta \leqslant 270^\circ ). And all other trigonometric functions are negative.
And, the value of cos⁡θ\cos \theta and sec⁡θ\sec \theta is positive if (270∘⩽θ⩽360∘270^\circ \leqslant \theta \leqslant 360^\circ ). And all other trigonometric functions are negative.
And we know that if 0∘⩽θ⩽90∘0^\circ \leqslant \theta \leqslant 90^\circ then,
⇒sin⁡(90∘+θ)=cos⁡θ\Rightarrow \sin \left( {90^\circ + \theta } \right) = \cos \theta
⇒cos⁡(90∘+θ)=−sin⁡θ\Rightarrow \cos \left( {90^\circ + \theta } \right) = - \sin \theta
⇒sin⁡(180∘+θ)=−sin⁡θ\Rightarrow \sin \left( {180^\circ + \theta } \right) = - \sin \theta
⇒cos⁡(180∘+θ)=−cos⁡θ\Rightarrow \cos \left( {180^\circ + \theta } \right) = - \cos \theta
⇒sin⁡(270∘+θ)=−cos⁡θ\Rightarrow \sin \left( {270^\circ + \theta } \right) = - \cos \theta
⇒cos⁡(270∘+θ)=sin⁡θ\Rightarrow \cos \left( {270^\circ + \theta } \right) = \sin \theta
Now we had to change all the angles of the equation to make them less than 90∘90^\circ .
So, we can write given equation as,
sin⁡(90∘+30∘)×cos⁡(90∘+60∘)−cos⁡(180∘+60∘)×sin⁡(270∘+60∘)\sin \left( {90^\circ + 30^\circ } \right) \times \cos \left( {90^\circ + 60^\circ } \right) - \cos \left( {180^\circ + 60^\circ } \right) \times \sin \left( {270^\circ + 60^\circ } \right)
Now solving the above equation using the above written statements.
cos⁡(30∘)×(−sin⁡(60∘))−(−cos⁡(60∘))×(−cos⁡(60∘))\cos \left( {30^\circ } \right) \times \left( { - \sin \left( {60^\circ } \right)} \right) - \left( { - \cos \left( {60^\circ } \right)} \right) \times \left( { - \cos \left( {60^\circ } \right)} \right) (1)
Now we know that cos⁡(30∘)\cos \left( {30^\circ } \right) = 32\dfrac{{\sqrt 3 }}{2}, sin⁡(60∘)\sin \left( {60^\circ } \right) = 32\dfrac{{\sqrt 3 }}{2} and cos⁡(60∘)\cos \left( {60^\circ } \right) = 12\dfrac{1}{2}
So, equation 1 becomes,
32×(−32)−(−12)×(−12)=−34−14=−44=−1\dfrac{{\sqrt 3 }}{2} \times \left( { - \dfrac{{\sqrt 3 }}{2}} \right) - \left( { - \dfrac{1}{2}} \right) \times \left( { - \dfrac{1}{2}} \right) = \dfrac{{ - 3}}{4} - \dfrac{1}{4} = \dfrac{{ - 4}}{4} = - 1
So, the value of the given trigonometric equation will be –1 .
Hence, the correct answer will be B.

Note: Whenever we come up with this type of trigonometric equation then we will make all angles less than 90∘90^\circ by applying trigonometric identities. And then put the value of cos⁡θ\cos \theta , sin⁡θ\sin \theta etc where \theta{\text{\theta }} is less than 90∘90^\circ , to get the required value of the given equation. And this will be the easiest and efficient way to find the solution of the problem.