Solveeit Logo
Login

Question

Question: Find the value of the expression \(\tan \left( {{120}^{\circ }} \right)\) \[\] A.\(1\) \[\] B.\(...

Find the value of the expression tan⁡(120∘)\tan \left( {{120}^{\circ }} \right) A.$1$
B.−1-1 C. $\sqrt{3}$
D.−3-\sqrt{3} $$$$

Explanation

Solution

We recall the sine, cosine and tangent trigonometric ratios in the right angled triangle. We find the value of sin⁡120∘,cos⁡120∘\sin {{120}^{\circ }},\cos {{120}^{\circ }} using the shift formulas sin⁡(θ+90∘)=cos⁡θ,cos⁡(θ+90∘)=−sin⁡θ\sin \left( \theta +{{90}^{\circ }} \right)=\cos \theta ,\cos \left( \theta +{{90}^{\circ }} \right)=-\sin \theta and use the trigonometric identity tan⁡θ=sin⁡θcos⁡θ\tan \theta =\dfrac{\sin \theta }{\cos \theta } for θ=120∘\theta ={{120}^{\circ }}.

Complete step-by-step solution:

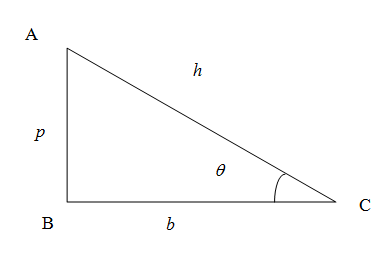
We know from the trigonometric ratios in a right angled triangle that the sine of any angle is given by the ratio of side length of opposite side to the angle to the length of hypotenuse. In the figure the sine of the angle θ\theta is given by
sin⁡θ=ph...(1)\sin \theta =\dfrac{p}{h}...(1)
Similarly the cosine of an angle is the ratio of length of side adjacent to the angle (excluding hypotenuse) to the hypotenuse. So we have cosine of angle θ\theta
cos⁡θ=bh...(2)\cos \theta =\dfrac{b}{h}...(2)
We know from the trigonometric ratios in a right angled triangle that the tangent of the angle is the ratio of length of opposite side to length of the adjacent side (excluding hypotenuse) to that angle. So we have tangent of the angle θ\theta as
tan⁡θ=pb\tan \theta =\dfrac{p}{b}
We have from (1) and (2) that
tan⁡θ=sin⁡θcos⁡θ\tan \theta =\dfrac{\sin \theta }{\cos \theta }
We know from the shift formula that when an acute angle θ\theta is turned by a right angle or quarter turn the trigonometric function for that angle θ\theta will be equal to the complimentary trigonometric function with argument θ\theta with possibly sign change. The shift formula for right angle or 90∘{{90}^{\circ }}turn is given by

& \Rightarrow \sin \left( \theta +{{90}^{\circ }} \right)=\cos \theta \\\ & \Rightarrow \cos \left( \theta +{{90}^{\circ }} \right)=-\sin \theta \\\ \end{aligned}$$ Let us take $\theta ={{30}^{\circ }}$ and have; $$\begin{aligned} & \Rightarrow \sin {{120}^{\circ }}=\sin \left( {{30}^{\circ }}+{{90}^{\circ }} \right)=\cos {{30}^{\circ }}=\dfrac{\sqrt{3}}{2} \\\ & \Rightarrow \cos {{120}^{\circ }}=\cos \left( \theta +{{90}^{\circ }} \right)=-\sin {{30}^{\circ }}=\dfrac{-1}{2} \\\ \end{aligned}$$ So we have the required value as $$\tan {{120}^{\circ }}=\dfrac{\sin {{120}^{\circ }}}{\cos {{120}^{\circ }}}=\dfrac{\dfrac{\sqrt{3}}{2}}{\dfrac{-1}{2}}=-\sqrt{3}$$ **So the correct option is D.** **Note:** We can directly use shift by ${{90}^{\circ }}$ formula for tangent function as $\tan \left( \theta +{{90}^{\circ }} \right)=-\cot \theta $ for $\theta ={{30}^{\circ }}$. We can also shift for odd integral times of ${{90}^{\circ }}$ and we shall get the same result as in shift for ${{90}^{\circ }}$.We must be careful of the confusion between shift forward formula from shift backward formula $\sin \left( \theta -{{90}^{\circ }} \right)=-\cos \theta ,\cos \left( \theta -{{90}^{\circ }} \right)=\sin \theta $ and also from the reduction formulas $\sin \left( {{90}^{\circ }}-\theta \right)=\cos \theta ,\cos \left( {{90}^{\circ }}-\theta \right)=\sin \theta $.