Question

Find the value of the expression given below,
$\sin 30{}^\circ \cos 60{}^\circ +\sin 60{}^\circ \cos 30{}^\circ$
[a] $\dfrac{1}{2}$
[b] $\dfrac{\sqrt{3}}{2}$
[c] 1
[d] $\dfrac{1}{4}$

Answer 1

Substitute the values of $\sin 30{}^\circ ,\sin 60{}^\circ ,\cos 30{}^\circ ,\cos 60{}^\circ$ and simplify and hence find the value of the given expression

Complete step-by-step answer:
To solve the given question, we need to remember the values of $\sin 30{}^\circ ,\sin 60{}^\circ ,\cos 30{}^\circ$ and $\cos 60{}^\circ$
Consider the following tables of values of sine, cosine, tangent, cotangent, secant and cosecant for angles of measure $0{}^\circ ,30{}^\circ ,45{}^\circ ,60{}^\circ ,90{}^\circ$

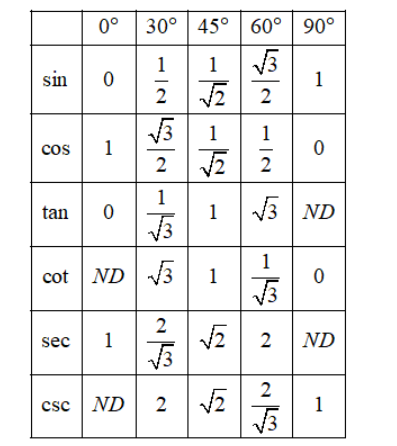
From the above table, we have
$\sin 30{}^\circ =\dfrac{1}{2},\sin 60{}^\circ =\dfrac{\sqrt{3}}{2},\cos 30{}^\circ =\dfrac{\sqrt{3}}{2},\cos 60{}^\circ =\dfrac{1}{2}$
Substituting the values of $\sin 30{}^\circ ,\sin 60{}^\circ ,\cos 30{}^\circ ,\cos 60{}^\circ$, we get
$S=\dfrac{1}{2}\times \dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\times \dfrac{\sqrt{3}}{2}$
Simplifying, we get
$S=\dfrac{1}{4}+\dfrac{3}{4}=\dfrac{4}{4}=1$
Hence, we have
$\sin 30{}^\circ \cos 60{}^\circ +\sin 60{}^\circ \cos 30{}^\circ$ is equal to 1.
Therefore the correct answer is option (c).

Note: [1] Alternatively, you can use the fact that $\cos \left( 90{}^\circ -\theta \right)=\sin \theta$ and $\sin \left( 90{}^\circ -\theta \right)=\cos \theta$ and then write $\cos 60{}^\circ$ as $\cos \left( 90{}^\circ -30{}^\circ \right)=\sin 30{}^\circ$ and $\sin 60{}^\circ$ as $\sin \left( 90{}^\circ -30{}^\circ \right)=\cos 30{}^\circ$
Hence the expression becomes
$S={{\sin }^{2}}30{}^\circ +{{\cos }^{2}}30{}^\circ$
Now, we know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$
Hence, we have
$S=1$, which is the same as obtained above.
Hence option [c] is the correct answer.
[2] Alternative
We know that $\sin A\cos B+\cos A\sin B=\sin \left( A+B \right)$
Put $A=30{}^\circ$ and $B=60{}^\circ$.
Hence, we have
$\sin \left( 30{}^\circ +60{}^\circ \right)=\sin 30{}^\circ \cos 60{}^\circ +\cos 30{}^\circ \sin 60{}^\circ =S$
Hence, we have
$S=\sin 90{}^\circ$
From the above table, we have $\sin 90{}^\circ =1$
Hence, we have $S=1$, which is the same as obtained above.
Hence option [c] is the correct answer.