Question

Find the value of tetrahedron V – ABC if V is (1, 1, 1), A is (1, 2, 3), B is (2, 3, 4) and C is (2, 3, - 1).

Answer 1

Hint: We will be using the basic concept of vectors and 3-D geometry to solve the problem. We will be using a scalar triple product of vectors to solve the problem.

Complete step by step answer:
We can draw the tetrahedron V – ABC as below,

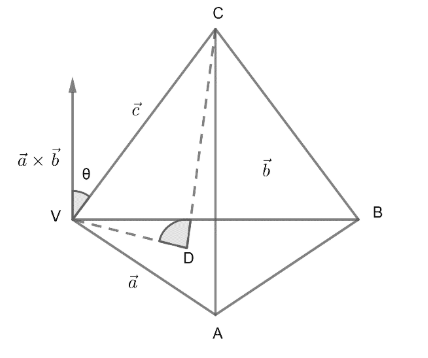
Here,
$\begin{aligned} & \overset{\to }{\mathop{VA}}\,=\overset{\to }{\mathop{a}}\, \\\ & \overset{\to }{\mathop{VB}}\,=\overset{\to }{\mathop{b}}\, \\\ & \overset{\to }{\mathop{VC}}\,=\overset{\to }{\mathop{c}}\, \\\ \end{aligned}$
Now, we have to find the volume of the tetrahedron. For this we know that,
The volume of tetrahedron $=\dfrac{1}{3}\left( base\times height \right).......\left( 1 \right)$
Now, we have to find the base of the tetrahedron. Considering $\Delta VAB$ as base. The base area can be written as $base=\dfrac{1}{2}\left| \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\, \right|$
Now, we have to find the height of the tetrahedron considering $\Delta VAB$ as base.
By taking $\Delta OAB$ as base. We can write height as $\left| \overset{\to }{\mathop{c}}\, \right|\cos \theta$, where $\theta$ is the angle between $\left( \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\, \right)\ and\ \overset{\to }{\mathop{c}}\,$.
So,
The volume of tetrahedron $=\dfrac{1}{3}\left( base\ area\times height \right)$

& =\dfrac{1}{3}\left( \dfrac{1}{2}\left| \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\, \right| \right)\left( \left| \overset{\to }{\mathop{c}}\, \right|\cos \theta \right) \\\ & =\dfrac{1}{6}\left| \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\, \right|\left| \overset{\to }{\mathop{c}}\, \right|\cos \theta \\\ & \text{Using }\overset{\to }{\mathop{A}}\,.\overset{\to }{\mathop{B}}\,=\overset{\to }{\mathop{A}}\,\overset{\to }{\mathop{B}}\,\cos \theta \\\ & =\dfrac{1}{6}\left( \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\,.\overset{\to }{\mathop{c}}\, \right) \\\ \end{aligned}$$ Now, we know that, $\begin{aligned} & \overset{\to }{\mathop{VA}}\,=\overset{\to }{\mathop{a}}\,=\left( 1-1 \right)\overset{\hat{\ }}{\mathop{i}}\,+\left( 2-1 \right)\overset{\hat{\ }}{\mathop{j}}\,+\left( 3-1 \right)\overset{\hat{\ }}{\mathop{k}}\, \\\ & \overset{\to }{\mathop{VB}}\,=\overset{\to }{\mathop{b}}\,=\left( 2-1 \right)\overset{\hat{\ }}{\mathop{i}}\,+\left( 3-1 \right)\overset{\hat{\ }}{\mathop{j}}\,+\left( 4-1 \right)\overset{\hat{\ }}{\mathop{k}}\, \\\ & \overset{\to }{\mathop{VC}}\,=\overset{\to }{\mathop{c}}\,=\left( 2-1 \right)\overset{\hat{\ }}{\mathop{i}}\,+\left( 3-1 \right)\overset{\hat{\ }}{\mathop{j}}\,+\left( -1-1 \right)\overset{\hat{\ }}{\mathop{k}}\, \\\ \end{aligned}$ Now, we that the vector triple product of three vectors, $\begin{aligned} & \overset{\to }{\mathop{a}}\,={{x}_{1}}\overset{\hat{\ }}{\mathop{i}}\,+{{y}_{1}}\overset{\hat{\ }}{\mathop{j}}\,+{{z}_{1}}\overset{\hat{\ }}{\mathop{k}}\, \\\ & \overset{\to }{\mathop{b}}\,={{x}_{2}}\overset{\hat{\ }}{\mathop{i}}\,+{{y}_{2}}\overset{\hat{\ }}{\mathop{j}}\,+{{z}_{2}}\overset{\hat{\ }}{\mathop{k}}\, \\\ & \overset{\to }{\mathop{c}}\,={{x}_{3}}\overset{\hat{\ }}{\mathop{i}}\,+{{y}_{3}}\overset{\hat{\ }}{\mathop{j}}\,+{{z}_{3}}\overset{\hat{\ }}{\mathop{k}}\, \\\ \end{aligned}$ It can be solved as a matrix. For example, $$\left( \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\,.\overset{\to }{\mathop{c}}\, \right)=\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & {{z}_{1}} \\\ {{x}_{2}} & {{y}_{2}} & {{z}_{2}} \\\ {{x}_{3}} & {{y}_{3}} & {{z}_{3}} \\\ \end{matrix} \right|$$ So, using this we can find the volume of tetrahedron as, $$\dfrac{1}{6}\left| \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\,.\overset{\to }{\mathop{c}}\, \right|=\dfrac{1}{6}\left| \begin{matrix} 0 & 1 & 2 \\\ 1 & 2 & 3 \\\ 1 & 2 & -2 \\\ \end{matrix} \right|$$ Now, we can expand the matrix along R as, $\begin{aligned} & 0\left( -4-6 \right)-1\left( -2-3 \right)+2\left( 2-2 \right) \\\ & -10-1\left( -5 \right)+2\left( 0 \right) \\\ & -10+5 \\\ & -5 \\\ \end{aligned}$ So, the volume of tetrahedron is, $\begin{aligned} & =\dfrac{1}{6}\left| -5 \right| \\\ & =\dfrac{5}{6} \\\ \end{aligned}$ Hence, $\dfrac{5}{6}$ is the volume of the given tetrahedron. Note: The question is calculation intensive. It is advised to do the calculation carefully also remembering some formula like that of finding volume of tetrahedron simplifies the problem to a great extent. Volume of tetrahedron $$=\dfrac{1}{2}\left( \overset{\to }{\mathop{a}}\,\times \overset{\to }{\mathop{b}}\,.\overset{\to }{\mathop{c}}\, \right)$$