Question

Find the value of $\sqrt {3.5}$ geometrically.

Answer 1

Here we will follow some basic steps to draw the required number. Below are the steps that need to follow:
To mark any number $\sqrt x$ on the number line, first of all, we will draw a line ${\text{AB}}$ of $x$ units.
After extending that line to $1$ unit till point ${\text{C}}$, we will find the midpoint of that particular line ${\text{AC}}$ which is $x + 1$ units, and marking it as point ${\text{E}}$
We will draw a semicircle after that taking ${\text{E}}$ as a Centre point and ${\text{AC}}$ as diameter.
After that, we will draw a perpendicular line from the point ${\text{B}}$, which cuts the semicircle at the point ${\text{D}}$.
So, ${\text{BD}}$ is required $\sqrt x$.

Complete step-by-step solution:
Step 1: For finding the value of
$\sqrt {3.5}$ first of all we will draw a line of
$3.5$ the unit as shown below:

Step 2: Now, by extending the line
${\text{PQ}}$ to $1$ the unit, we get:

Step 3: Now we will find the midpoint of
${\text{PR = 4}}{\text{.5 unit}}$, which is a point
${\text{S}}$, by using the scale or by drawing the bisector of that line such that ${\text{PS = SR = 2}}{\text{.25 unit}}$, as shown below:

Step 4: Now, by drawing a semicircle taking
${\text{S}}$ as a Centre point and ${\text{PR}}$ as diameter, we get the below figure:

Step 5: Now by drawing a perpendicular line from the point
${\text{Q}}$ which cuts the semi-circle at the point ${\text{T}}$, we get the below figure:

Step 6: Now, the line
${\text{QT}}$ is our required line of $\sqrt {3.5}$ the unit.
Answer/Conclusion:
$\because$ Our required figure is as below:

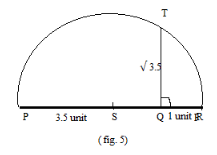
Note: Students can follow the below proof for calculating the value of any number
$\sqrt x$ geometrically for their better understanding:
First of all, we will draw a line ${\text{AB}}$ of $x$ units. After extending that line to $1$ unit till point ${\text{C}}$, we will find the midpoint of that particular line ${\text{AC}}$ which is $x + 1$ units and marking it as a point ${\text{E}}$. We will draw a semicircle after that taking ${\text{E}}$ as a Centre point and ${\text{AC}}$ as diameter. After that we will draw a perpendicular line from the point ${\text{B}}$, which cuts the semicircle at the point ${\text{D}}$ as shown in the below diagram:

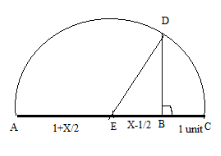
In the above diagram, we know that ${\text{AC = }}x + 1$. Because ${\text{E}}$ is the midpoint of the line ${\text{AC}}$ then, ${\text{AE = }}\left( {\dfrac{{x + 1}}{2}} \right)$ and similarly we will find the value of ${\text{EB}}$ as shown below:
$\Rightarrow {\text{EB = AB - AE}}$
By substituting the value of ${\text{AE = }}\left( {\dfrac{{x + 1}}{2}} \right)$ and ${\text{AB = }}x$ in the above expression, we get:
$\Rightarrow {\text{EB = }}x{\text{ - }}\left( {\dfrac{{x + 1}}{2}} \right)$
By simplifying the above expression, we get:
$\Rightarrow {\text{EB = }}\left( {\dfrac{{x - 1}}{2}} \right)$
Now, by using Pythagoras theorem $\Delta {\text{EDB}}$, we get:
$\Rightarrow {\left( {{\text{ED}}} \right)^2} = {\left( {{\text{EB}}} \right)^2} + {\left( {{\text{BD}}} \right)^2}$
By substituting the values of ${\text{EB = }}\left( {\dfrac{{x - 1}}{2}} \right)$ and ${\text{ED = }}\left( {\dfrac{{x + 1}}{2}} \right)$, because ${\text{ED}}$is the radius of the circle, we get:
$\Rightarrow {\left( {\dfrac{{1 + x}}{2}} \right)^2} = {\left( {\dfrac{{x - 1}}{2}} \right)^2} + {\left( {{\text{BD}}} \right)^2}$
By bringing ${\left( {\dfrac{{x - 1}}{2}} \right)^2}$ into the LHS side of the expression, we get:
$\Rightarrow {\left( {\dfrac{{1 + x}}{2}} \right)^2} - {\left( {\dfrac{{x - 1}}{2}} \right)^2} = {\left( {{\text{BD}}} \right)^2}$
By subtracting into the LHS side of the above expression we get:
$\Rightarrow \dfrac{{1 + {x^2} + 2x - {x^2} - 1 + 2x}}{4} = {\left( {{\text{BD}}} \right)^2}$
By simplifying the numerator of the term $\dfrac{{1 + {x^2} + 2x - {x^2} - 1 + 2x}}{4}$ , we get:
$\Rightarrow \dfrac{{4x}}{4} = {\left( {{\text{BD}}} \right)^2}$
By eliminating $4$ from the LHS side of the expression we get:
$\Rightarrow x = {\left( {{\text{BD}}} \right)^2}$
By taking root on both sides of the above expression, we get:
$\Rightarrow \sqrt x = {\text{BD}}$
Hence proved.