Solveeit Logo
Login

Question

Question: Find the value of \( \sin {{60}^{\circ }}\csc {{60}^{\circ }} \) ....

Find the value of sin⁡60∘csc⁡60∘\sin {{60}^{\circ }}\csc {{60}^{\circ }} .

Explanation

Solution

Hint : In order to solve this problem, we need to understand the meaning of terms of sin and csc.The sin angle is defined as the ratio of the side opposite the angle and the hypotenuse. The csc angle is defined as the ratio of the hypotenuse to the side opposite to the angle. After finding the ratios of both with the help of the example we can find the product between the two ratios.

Complete step-by-step answer :
We have been asked to find the value of sin⁡60∘csc⁡60∘\sin {{60}^{\circ }}\csc {{60}^{\circ }} .
All the trigonometric ratios are derived from the based on the right angle triangle.
Let's first understand the terms sin and csc.
Also, csc can be said as cosec, either way, it’s the same thing.
Consider a ΔABC\Delta ABC .

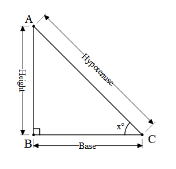
We can see that ∠ABC=90∘\angle ABC={{90}^{\circ }} and AB = height , BC = base, AC = hypotenuse.
The sin angle is defined as the ratio of the side opposite the angle and the hypotenuse.
In this case, we consider the angle x∘{{x}^{\circ }} , therefore, the side opposite of this is height.
So, sin⁡x∘=heighthypotenuse....................(i)\sin {{x}^{\circ }}=\dfrac{\text{height}}{\text{hypotenuse}}....................(i)
Similarly, the csc angle is defined as the ratio of the hypotenuse to the side opposite to the angle.
So, csc⁡x∘=hypotenuseheight.........................(ii)\csc {{x}^{\circ }}=\dfrac{\text{hypotenuse}}{\text{height}}.........................(ii)
Multiplying equation (i) with equation (ii), we get,
sin⁡x∘×csc⁡x∘=heighthypotenuse×hypotenuseheight\sin {{x}^{\circ }}\times \csc {{x}^{\circ }}=\dfrac{\text{height}}{\text{hypotenuse}}\times \dfrac{\text{hypotenuse}}{\text{height}}
Solving this we get,
sin⁡x∘×csc⁡x∘=1\sin {{x}^{\circ }}\times \csc {{x}^{\circ }}=1
As we can see that the product is independent of the angle.
So the value of sin⁡60∘×csc⁡60∘=1\sin {{60}^{\circ }}\times \csc {{60}^{\circ }}=1 .

Note : We can solve this with a different approach. We can find the values of sin⁡60∘\sin {{60}^{\circ }} and csc⁡60∘\csc {{60}^{\circ }} separately and multiply them. The value of sin⁡60∘\sin {{60}^{\circ }} is 32\dfrac{\sqrt{3}}{2} . The value of csc⁡60∘\csc {{60}^{\circ }} is 233\dfrac{2\sqrt{3}}{3} .
By multiplying we get,
sin⁡60∘×csc⁡60∘=32×233=1\sin {{60}^{\circ }}\times \csc {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}\times \dfrac{2\sqrt{3}}{3}=1 . Hence we get the same answer.