Question

Find the value of: $\sin {{120}^{\circ }}\cos {{150}^{\circ }}+\cos {{240}^{\circ }}\sin {{330}^{\circ }}=?$

Answer 1

Hint: We can solve this using quadrants, take each value and find which quadrant it belongs to and simplify it. When all the simplified values are found, use the trigonometric table to get the value of the function.
Complete step-by-step answer:

Let us use the ASTC rules to determine the sign of the ratio and quadrant expressions. Let us consider the original angle given as $\theta$ and the auxiliary value as $\alpha$, this can be generated according to the quadrant taken.
For quadrant II, we can write that, $\theta =180-\alpha$.
For quadrant III, we can write that, $\theta =180+\alpha$.
For quadrant IV, we can write that, $\theta =360-\alpha$.

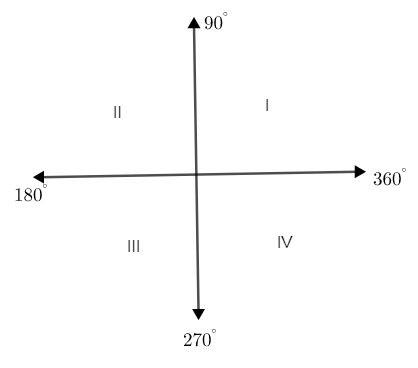
Now let us take our ${{1}^{st}}$ value, $\sin {{120}^{\circ }}$.
${{120}^{\circ }}$ lies in the II quadrant.
$\therefore \sin {{120}^{\circ }}=\sin \left( 180-\alpha \right)=\sin \left( 180-{{60}^{\circ }} \right)$
In quadrant II, sine is positive hence,
$\therefore \sin {{120}^{\circ }}=\sin \left( 180-\alpha \right)=\sin \left( 180-{{60}^{\circ }} \right)=\sin {{60}^{\circ }}$
Now let us consider out ${{2}^{nd}}$ value, $\cos {{150}^{\circ }}$.
It lies in quadrant II and the value of cosine is negative in II quadrant.
$\cos {{150}^{\circ }}=\cos \left( 180-\alpha \right)$
$\begin{aligned} & =\cos \left( 180-30 \right) \\\ & =-\cos {{30}^{\circ }} \\\ \end{aligned}$
$\therefore \cos {{150}^{\circ }}=-\cos {{30}^{\circ }}$
Now let us consider $\cos {{240}^{\circ }}$. ${{240}^{\circ }}$ lies in the ${{3}^{rd}}$ quadrant. Cosine function is negative in the ${{3}^{rd}}$ quadrant.
$\therefore \cos {{240}^{\circ }}=\cos \left( 180+\alpha \right)$
$\begin{aligned} & =-\cos \left( 180+{{60}^{\circ }} \right) \\\ & =-\cos {{60}^{\circ }} \\\ \end{aligned}$
$\therefore \cos {{240}^{\circ }}=-\cos {{60}^{\circ }}$
Similarly, $\sin {{330}^{\circ }}$, ${{330}^{\circ }}$ lies in the ${{4}^{th}}$ quadrant. Sine function is negative in the ${{4}^{th}}$ quadrant.
$\sin {{330}^{\circ }}=\sin \left( 360-\alpha \right)$
$\begin{aligned} & =-\sin \left( 360-{{30}^{\circ }} \right) \\\ & =-\sin {{30}^{\circ }} \\\ \end{aligned}$
$\therefore \sin {{330}^{\circ }}=-\sin {{30}^{\circ }}$
Hence, we can write that,

& \sin {{120}^{\circ }}\cos {{150}^{\circ }}+\cos {{240}^{\circ }}\sin {{330}^{\circ }} \\\ & =\sin {{60}^{\circ }}\times \left( -\cos {{30}^{\circ }} \right)+\left( -\cos {{60}^{\circ }} \right)\times \left( -\sin {{30}^{\circ }} \right) \\\ & =-\sin {{60}^{\circ }}\cos {{30}^{\circ }}+\cos {{60}^{\circ }}\sin {{30}^{\circ }} \\\ \end{aligned}$$ From the trigonometric table, we can find the values as, $$\theta $$| $${{0}^{\circ }}$$| $${{30}^{\circ }}$$| $${{45}^{\circ }}$$| $${{60}^{\circ }}$$| $${{90}^{\circ }}$$ ---|---|---|---|---|--- sin| 0| $$\dfrac{1}{2}$$| $$\dfrac{1}{\sqrt{2}}$$| $$\dfrac{\sqrt{3}}{2}$$| 1 cos| 1| $$\dfrac{\sqrt{3}}{2}$$| $$\dfrac{1}{\sqrt{2}}$$| $$\dfrac{1}{2}$$| 0 tan| 0| $$\dfrac{1}{\sqrt{3}}$$| 1| $$\sqrt{3}$$| N.A cosec| N.A| 2| $$\sqrt{2}$$| $$\dfrac{2}{\sqrt{3}}$$| 1 sec| 1| $$\dfrac{2}{\sqrt{3}}$$| $$\sqrt{2}$$| 2| N.A cot| N.A| $$\sqrt{3}$$| 1| $$\dfrac{1}{\sqrt{3}}$$| 0 From the table we can say that, $$\begin{aligned} & \sin 60=\dfrac{\sqrt{3}}{2} \\\ & \cos 30=\dfrac{\sqrt{3}}{2} \\\ & \cos 60=\dfrac{1}{2} \\\ & \sin 30=\dfrac{1}{2} \\\ \end{aligned}$$ $$\begin{aligned} & \therefore -\sin {{60}^{\circ }}\times \cos {{30}^{\circ }}+\cos {{60}^{\circ }}\sin {{30}^{\circ }} \\\ & =-\left( \dfrac{\sqrt{3}}{2}\times \dfrac{\sqrt{3}}{2} \right)+\left( \dfrac{1}{2}\times \dfrac{1}{2} \right) \\\ & =-\dfrac{3}{4}+\dfrac{1}{4}=\dfrac{-3+1}{4}=\dfrac{-2}{4} \\\ & =\dfrac{-1}{2} \\\ \end{aligned}$$ Thus we got, $$\sin {{120}^{\circ }}\cos {{150}^{\circ }}+\cos {{240}^{\circ }}\sin {{330}^{\circ }}=\dfrac{-1}{2}$$. $$\therefore $$ We got the required value. Note: Remember the basics of quadrant that, In Quadrant I: All functions are positive. In Quadrant II: $$\sin \theta $$ and $$\csc \theta $$ are positive. In Quadrant III: $$\tan \theta $$ and $$\cot \theta $$ are positive. In quadrant IV: $$\cos \theta $$ and $$\sec \theta $$ are positive.