Question

Find the value of ${R_{net}}$ between $A$ and $B$.

A) $40$
B) $60$
C) $70$
D) $20$

Answer 1

First use the series combination of ${R_1},{R_2},{R_3}$ to find the values of ${R_{s1}}$. Now these ${R_{s1}}$ will be become parallel combination with ${R_4}$ .Then calculate the value of ${R_{p1}}$ . after that ${R_5},{R_6}$ and ${R_{p1}}$ are in series combination, So calculate the value of ${R_{s2}}$ .Now ${R_7},{R_{s2}}$ are in parallel combination, Therefore we have to find the value of ${R_{p2}}$ now ${R_8},{R_9}$ and ${R_{p2}}$ are in series combination than after we calculate ${R_{net}}$.

Complete step by step solution:
Let us consider the following diagram

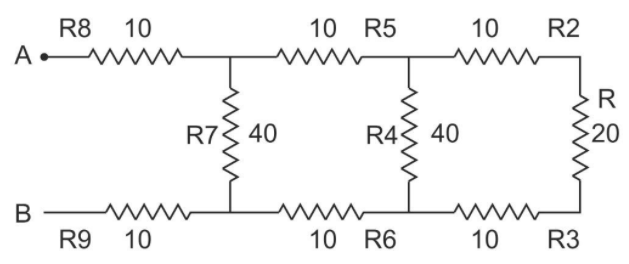
First, we must calculate ${R_{s1}}$
In this question, the given that,
Resistance
${R_1} = 20 \\\ {R_2} = 10 \\\ {R_3} = 10 \\\$

Since these resistances are in series combination, So we will use the series combination formula that is,
$\Rightarrow {R_{s1}} = {R_1} + {R_2} + {R_3}$

On putting the value of these resistance we get,
$\Rightarrow {R_{s1}} = 20 + 10 + 10$
After calculation we will get,
$\Rightarrow {R_{s1}} = 40$

Now, ${R_{s1}}$ will become a parallel combination with ${R_4}$.

We know that parallel combination formula is
$\Rightarrow \dfrac{1}{{{R_{p1}}}} = \dfrac{1}{{{R_4}}} + \dfrac{1}{{{R_{s1}}}}$

On putting the value of these resistance we get,
$\Rightarrow \dfrac{1}{{{R_{p1}}}} = \dfrac{1}{{40}} + \dfrac{1}{{40}}$
After calculation we will get,
$\Rightarrow \dfrac{1}{{{R_{p1}}}} = \dfrac{2}{{40}}$
$\Rightarrow \dfrac{1}{{{R_{p1}}}} = \dfrac{1}{{20}}$
Take the reciprocal on both side we get,
${R_{p1}} = 20$

Now we have to calculate the value of ${R_{s2}}$ with the series combination of ${R_5},{R_6},{R_{p1}}$
Using the series combination formula, we get, ${R_{s2}} = {R_5} + {R_6} + {R_{p1}}$

On putting the values of these resistances, we find that,
$\Rightarrow {R_{s2}} = 10 + 10 + 20$
$\Rightarrow {R_{s2}} = 40$
Now ${R_{s2}},{R_7}$ are in parallel combination, So we have calculate the value of ${R_{p2}}$ by using the parallel combination formula that is,

$$\dfrac{1}{{{R_{p2}}}} = \dfrac{1}{{{R_7}}} + \dfrac{1}{{{R_{s2}}}} \\\ \\\$$

On putting these value, we get,
$\dfrac{1}{{{R_{p2}}}} = \dfrac{1}{{40}} + \dfrac{1}{{40}} \\\ \Rightarrow \dfrac{1}{{{R_{p2}}}} = \dfrac{2}{{40}} \\\ \Rightarrow \dfrac{1}{{{R_{p2}}}} = \dfrac{1}{{20}} \\\$

Taking the reciprocal on both side we get,
$\therefore {R_{p2}} = 20$

Now we have to calculate final the value of ${R_{net}}$ which are in series combination with ${R_8},{R_9},{R_{p2}}$

On putting the values of these we get,
$\Rightarrow {R_{net}} = 10 + 10 + 20$
After calculation we will get,
$\therefore {R_{net}} = 40$

Therefore, option (A) is the correct option.

Note: As we know that if the resistance is in series, the net resistance of the circuit will increase or if the resistance is in parallel than the resistance of the circuit decreases. So, these combinations are used on the requirement.