Question

Find the value of other five trigonometric ratios:
$\cot x = \dfrac{3}{4}$ , x lies in the third quadrant.

Answer 1

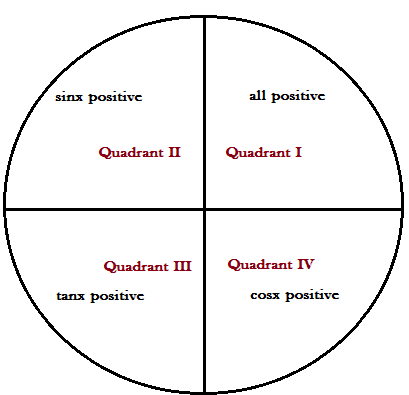
Given that x lies in third quadrant. Now if x lies in the third quadrant, only $\tan x$ and $\cot x$ is positive.
Also, note the following important formulae:
$\cos x = \dfrac{1}{{\sec x}}$ , $\sin x = \dfrac{1}{{\cos ecx}}$ , $\tan x = \dfrac{1}{{\cot x}}$
${\sin ^2}x + {\cos ^2}x = 1$
${\sec ^2}x - {\tan ^2}x = 1$
${\operatorname{cosec} ^2}x - {\cot ^2}x = 1$
Now, the value of $\cot x$ is given. Therefore find the value of the other five trigonometric ratios with the help of before mentioned formulae.

Complete step-by-step answer:
Given, $\cot x = \dfrac{3}{4}$
Therefore $\tan x = \dfrac{1}{{\cot x}} = \dfrac{4}{3}$
$\because {\sec ^2}x - {\tan ^2}x = 1$, we get,
$\Rightarrow {\sec ^2}x = 1 + {\tan ^2}x$
On taking square root we get,
$\Rightarrow \sec x = \pm \sqrt {1 + {{\tan }^2}x}$
On substituting the value of $\tan x$we get,
$\Rightarrow \sec x = \pm \sqrt {1 + {{\left( {\dfrac{4}{3}} \right)}^2}}$
On simplification we get,
$\Rightarrow \sec x = - \dfrac{5}{3}$
Here as, x lies in the third Quadrant, therefore $\sec x$ is negative.
Therefore $\cos x = \dfrac{1}{{\sec x}} = - \dfrac{3}{5}$
Again,
${\sin ^2}x + {\cos ^2}x = 1$
$\Rightarrow {\sin ^2}x = 1 - {\cos ^2}x$
On taking square root we get,
$\Rightarrow \sin x = \pm \sqrt {1 - {{\cos }^2}x}$
On substituting the value of $\cos x$we get,
$\Rightarrow \sin x = \pm \sqrt {1 - {{\left( { - \dfrac{3}{5}} \right)}^2}}$
On solving we get,
$\Rightarrow \sin x = \pm \sqrt {1 - \dfrac{9}{{25}}} = \pm \sqrt {\dfrac{{16}}{{25}}}$
On simplification we get,
$\Rightarrow \sin x = - \dfrac{4}{5}$
Here as, x lies in the third quadrant so the value of$\;\sin x$ will be negative.
Therefore, $\operatorname{cosecx} = \dfrac{1}{{\sin x}} = - \dfrac{5}{4}$
Hence when $\cot x = \dfrac{3}{4}$ , and x lies in third quadrant, the other five trigonometric ratios are :
$\tan x = \dfrac{4}{3}$, $\sin x = - \dfrac{4}{5}$ , $\cos x = - \dfrac{3}{5}$, $\sec x = - \dfrac{5}{3}$ and $\operatorname{cosecx} = - \dfrac{5}{4}$

Note: Note the following important formulae:
1.$\cos x = \dfrac{1}{{\sec x}}$ , $\sin x = \dfrac{1}{{\cos ecx}}$ , $\tan x = \dfrac{1}{{\cot x}}$
2.${\sin ^2}x + {\cos ^2}x = 1$
3.${\sec ^2}x - {\tan ^2}x = 1$
4.${\operatorname{cosec} ^2}x - {\cot ^2}x = 1$
5.$\sin ( - x) = - \sin x$
6.$\cos ( - x) = \cos x$
7.$\tan ( - x) = - \tan x$
8.$\sin \left( {2n\pi \pm x} \right) = \sin x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
9.$\cos \left( {2n\pi \pm x} \right) = \cos x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
10.$\tan \left( {n\pi \pm x} \right) = \tan x{\text{ , period }}\pi {\text{ or 18}}{0^ \circ }$
Sign convention: