Question

Find the value of $\operatorname{cosec} ( - {1410^ \circ })$

Answer 1

We know that ${\text{cosec}}\left( { - \theta } \right) = - {\text{cosec}}\theta$
Again, the function $y = \cos ecx$ has a period of $2\pi$ or $360^\circ$, i.e. the value of $\cos ecx\;$ repeats after an interval of $2\pi$ or $360^\circ$.
Therefore write $1410^\circ$ as $(4 \times 2\pi - 30^\circ )$ and proceed.

Complete step-by-step answer:
We know that the function $y = \cos ecx$ has a period of $2\pi$ or $360^\circ$, i.e. the value of $\cos ecx\;$ repeats after an interval of $2\pi$ or $360^\circ$.

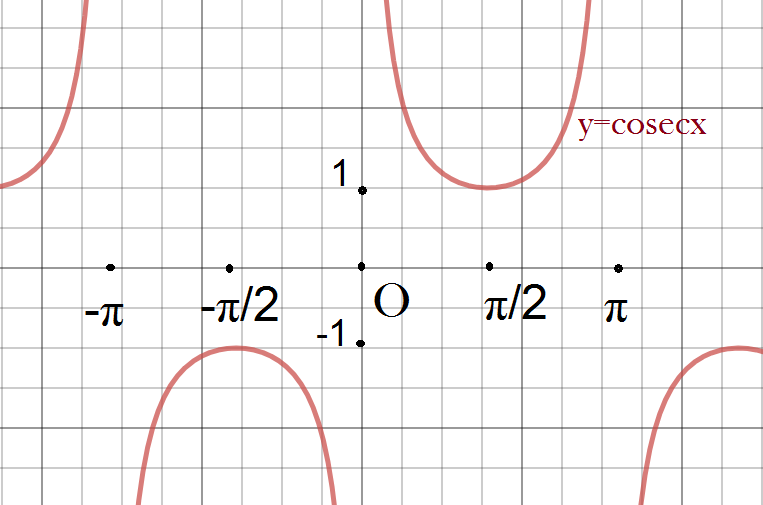
Therefore,
$\operatorname{cosec} ( - {1410^ \circ })$
Using, $\left[ {{\text{cosec}}\left( { - \theta } \right) = - {\text{cosec}}\theta } \right]$, we get,
$= - \operatorname{cosec} ({1410^ \circ }){\text{ }}$
We can write the above statement as,
$= - \operatorname{cosec} \left( {(4 \times {{360}^ \circ }) - {{30}^ \circ }} \right)$
Since ${\text{141}}{0^ \circ }$ lies in the fourth quadrant, therefore is ${\text{cosec141}}{0^ \circ }$ negative
$= - \left( { - \operatorname{cosec} {{30}^ \circ }} \right){\text{ }}$
$= \operatorname{cosec} {30^ \circ }$
As, $\operatorname{cosec} ({30^ \circ }) = 2$, we get,
$= 2$
Hence, the value of $\operatorname{cosec} ( - {1410^ \circ })$ is 2.

Note: Note the following important formulae:
1.$\cos x = \dfrac{1}{{\sec x}}$ , $\sin x = \dfrac{1}{{\cos ecx}}$ , $\tan x = \dfrac{1}{{\cot x}}$
2.${\sin ^2}x + {\cos ^2}x = 1$
3.${\sec ^2}x - {\tan ^2}x = 1$
4.${\operatorname{cosec} ^2}x - {\cot ^2}x = 1$
5.$\sin ( - x) = - \sin x$
6.$\cos ( - x) = \cos x$
7.$\tan ( - x) = - \tan x$
8.$\sin \left( {2n\pi \pm x} \right) = \sin x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
9.$\cos \left( {2n\pi \pm x} \right) = \cos x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
10.$\tan \left( {n\pi \pm x} \right) = \tan x{\text{ , period }}\pi {\text{ or 18}}{0^ \circ }$
Sign convention:

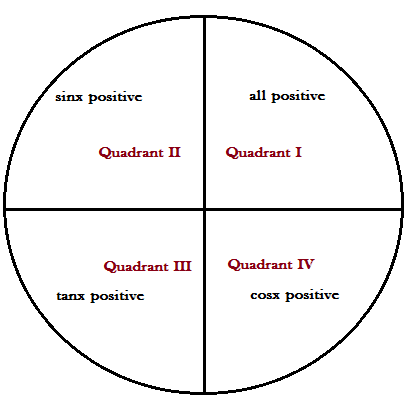
Also, the trigonometric ratios of the standard angles are given by

| $0^\circ$| $30^\circ$| $45^\circ$| $60^\circ$| $90^\circ$
---|---|---|---|---|---
$\operatorname{Sin} x$| 0| $\dfrac{1}{2}$ | $\dfrac{1}{{\sqrt 2 }}$ | $\dfrac{{\sqrt 3 }}{2}$ | 1
$\cos x$| 1| $\dfrac{{\sqrt 3 }}{2}$| $\dfrac{1}{{\sqrt 2 }}$| $\dfrac{1}{2}$| 0
$\tan x$| 0| $\dfrac{1}{{\sqrt 3 }}$ | 1| $\sqrt 3$| Undefined
$cotx$| undefined| $\sqrt 3$| 1| $\dfrac{1}{{\sqrt 3 }}$| 0
$\cos ecx\;$| undefined| 2| $\sqrt 2$| $\dfrac{2}{{\sqrt 3 }}$| 1
$\operatorname{Sec} x$| 1| $\dfrac{2}{{\sqrt 3 }}$| $\sqrt 2$| 2| Undefined