Question

Find the value of k so that the area of triangle ABC with A $\left( {k + 1,{\text{ }}1} \right),{\text{ }}B{\text{ }}\left( {4,{\text{ }} - 3} \right),{\text{ }}and{\text{ }}C{\text{ }}\left( {7,{\text{ }} - k} \right)$, is $6$ square units.

Answer 1

Hint : In this question to find the value of we will use this formula to calculate area of triangle$=$
$\dfrac{1}{2}|{x_1}({y_2} - {y_3}) + {x_2}({y_3} - {y_1}) + {x_3}({y_1} - {y_2})|$ and get the value of k.

Complete step-by-step answer :
We are given that area of triangle $ABC$
$= {\text{ }}6{\text{ }}sq.{\text{ }}units.$

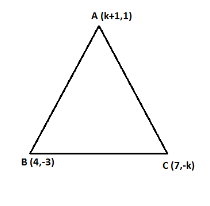
And co-ordinate are as follows
${x_1} = k + 1 \\\ {x_2} = 4 \\\ {x_3} = 7 \\\ {y_1} = 1 \\\ {y_2} = - 3 \\\ {y_3} = - k \\\$
where, A $\left( {k + 1,{\text{ }}1} \right),{\text{ }}B{\text{ }}\left( {4,{\text{ }} - 3} \right),{\text{ }}and{\text{ }}C{\text{ }}\left( {7,{\text{ }} - k} \right)$
$\Rightarrow \text{Area of triangle ABC} = \dfrac{1}{2}|{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_2}} \right)$
$\Rightarrow 6 = \dfrac{1}{2}\left| {\left( {k + 1} \right)\left( { - 3 + k} \right) + 4\left( { - k - 1} \right) + 7\left( {1 + 3} \right)} \right|$
$12 = \left| {{k^2} - 2k - 3 - 4k + 24} \right|$
$12 = \left| {{k^2} - 6k + 21} \right|$
$case:\left( 1 \right)$
$12 = {k^2} - 6k + 21$
${k^2} - 6k + 9 = 0$
$k = 3$
$case:\left( 2 \right)$
$- 12 = {k^2} - 6k + 21$
${k^2} - 6k + 33 = 0$
$D = {b^2} - 4ac$
$= \left( {36 - 4 \times 1 \times 33} \right) < 0$
So, it does not have real roots
Hence value of k $= {\text{ }}3.$

Note : Students should keep in mind that area is given $6{\text{ }}sq.$units, but we must use $+ 6$ and $- 6$ both the values to calculate k. Mostly, students miss this. Also, formulas for the area of the triangle should be learned.