Question

Find the value of $K$, if $\left( {1, - 1} \right)$ is a solution of the equation $3x - ky = 8$, Also find the coordinates of another point lying on its graph.

Answer 1

Hint: In this question put $\left( {1, - 1} \right)$in $3x - ky = 8$ and for coordinates let $x = 0$ in first case and $y = 0$ . Use this to find the coordinates of another point lying on its graph and the value of $K$.

Complete step-by-step solution -

__

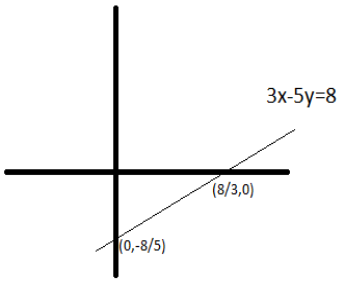
According to the question a equation $3x - ky = 8$ is given Hence $3x - ky = 8$
Put $\left( {1, - 1} \right)$ in it
$\Rightarrow 3 + k = 8 \\\ \Rightarrow k = 5 \\\$
Now another point on this $3x - ky = 8$
To find the coordinates of another point lying on graph
Let $x = 0$ and find $y$ coordinates
$\Rightarrow 3 \times 0 - \left( 5 \right) \times y = 8 \\\ \Rightarrow - 5y = 8 \\\ \Rightarrow y = \dfrac{{ - 8}}{5} \\\$
Coordinates $Q\left( {0,\dfrac{{ - 8}}{5}} \right)$ will lie on the graph.
Hence for another point lying on graph
Let $y = 0$ and find $x$ coordinates
$\Rightarrow 3x - \left( 5 \right) \times 0 = 8 \\\ \Rightarrow 3x = 8 \\\ \Rightarrow x = \dfrac{8}{3} \\\$
Coordinates $Q\left( {\dfrac{8}{3},0} \right)$ will lie on the graph .
Hence coordinates are $\left( {0,\dfrac{{ - 8}}{5}} \right),\left( {\dfrac{8}{3},0} \right)$.

Note: In such types of questions after finding the coordinates we have to draw a graphical representation of linear equation in two variables which is a system of linear equations that forms two straight lines .