Question
Question: Find the value of \(I\) ? A.\[\text{-1}\text{.4 A}\] B.\[\text{-2}\text{.1 A}\] C.\[\text{2A}\...
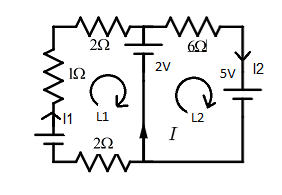
Find the value of I ?
A.-1.4 A
B.-2.1 A
C.2A
D.-4.2 A
Solution
Hint: The value of I can be found using Kirchhoff’s laws. Assume the directions of current and solve the Kirchhoff equations. Negative sign in the current implies the current flows in the opposite direction.
Formula used: V=IR (Ohm's law).
Complete solution Step-by-Step:
Kirchhoff’s Current Law or Kirchhoff’s First Law or Kirchhoff’s Junction Rule, states that in a circuit, the total of the currents in a junction is equal to the sum of currents outside the junction.
Kirchhoff’s Voltage Law or Kirchhoff’s Second Law or Kirchhoff’s Loop Rule. According to the loop rule, the sum of the voltages around the closed loop is equal to null.
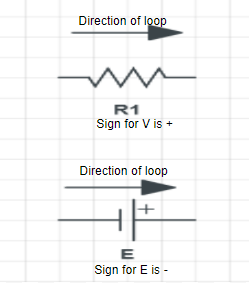
Defining the conventions:
According to Kirchhoff’s Current Law :I1+I=I2;I2−I1=I
According to Kirchhoff’s Voltage Law:
Sum of voltages is zero, from Ohm’s law V=IR, hence
In L1: 10−I1−2I1−2−2I1=0
8−5I1=0
8=5I1
I1=1.6
In L2:−6I2−5+2=0
−6I2−3=0
−6I2=3
I2=−0.5
Hence I in the circuit is given by
I2−I1=I using Kirchhoff’s Current Law
−0.5−1.6=I
−2.1=I in ampere
Hence B.-2.1 A is the answer.
Additional Information: In 1845, a German physicist, Gustav Kirchhoff developed a pair of laws that deal with the conservation of current and energy within electrical circuits. These two laws are commonly known as Kirchhoff’s Voltage and Current Law. The advantages of the laws are:
(I) It makes the calculation of unknown voltages and currents easy.
(II) The analysis and simplification of complex closed-loop circuits becomes manageable.
Note: Assume the directions of current and solve the Kirchhoff equations.Negative sign in the current implies the current flows in the opposite direction. Also take care of the sign convention. Loops can be clockwise or anticlockwise. Use V=IROhm's law.
