Question

Find the value of expression [x-y] for ${{\left( B{{F}_{2}} \right)}_{2}}B{{\left( B{{F}_{2}} \right)}_{2}}B{{\left( B{{F}_{2}} \right)}_{2}}$ where
x = maximum number of atoms that can lie in a plane.
y = number of ‘F’ atoms participating in back bonding.

Answer 1

The required value would be the difference between the maximum number of atoms that can lie in a plane and the number of ‘F’ atoms participating in back bonding.

Complete step by step solution:
Let us see the higher halides of boron which would eventually lead us to the required answer. The higher halide mentioned here is ${{\left( B{{F}_{2}} \right)}_{2}}B{{\left( B{{F}_{2}} \right)}_{2}}B{{\left( B{{F}_{2}} \right)}_{2}}$, this can be analysed by knowing about its structure.
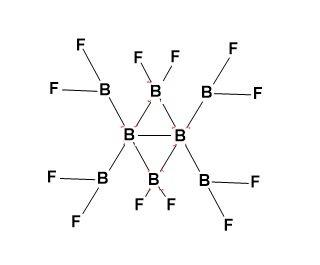
-${{\left( B{{F}_{2}} \right)}_{2}}B{{\left( B{{F}_{2}} \right)}_{2}}B{{\left( B{{F}_{2}} \right)}_{2}}$ structure has been shown by gas electron diffraction and computational methods.
-${{B}_{8}}{{F}_{12}}$ structure is assymetrical.
-The ${{B}_{8}}{{F}_{12}}$ structure is basically derived from a central ${{B}_{2}}$group which is bridged by two $B{{F}_{2}}$ groups to give central ${{B}_{4}}$ core (folded and non-planar).
-There are four terminal $B{{F}_{2}}$ groups.
Structure-

The presence of back bonding can be explained as;
Back-bonding- It is the sharing of electrons between the atomic orbital on one atom with an antibonding ${{\pi }^{*}}$ orbital on another atom. Back-bonding is also known as $\pi$ coordinate bond. Compounds showing back-bonding are of two types i.e.
a. Compounds in which side atoms are donating electron pairs to the central atom.
b. Compounds in which the central atom is donating electron pairs to the side atoms.
The ${{B}_{8}}{{F}_{12}}$ structure can be explained as,

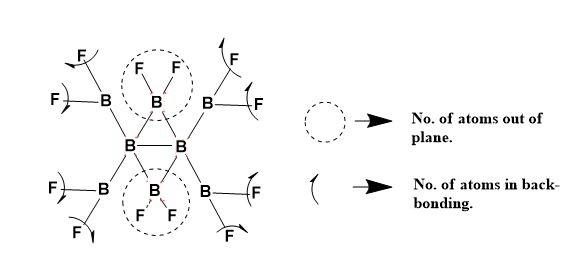
Thus, Number of atoms that can lie in a plane is 14.
Number of atoms participating in back-bonding are 8.
Therefore, The value of expression [x-y] for ${{\left( B{{F}_{2}} \right)}_{2}}B{{\left( B{{F}_{2}} \right)}_{2}}B{{\left( B{{F}_{2}} \right)}_{2}}$
where, x = maximum number of atoms that can lie in a plane.
y = number of ‘F’ atoms participating in back bonding is as: [x-y] = 14-8 = 6.

Note: Back-bonding is only possible when one atom in a compound has a lone pair of electrons and another has vacant orbital placed adjacent to each other. Also, one atom should be from the second period and the other should be from the third period. Do note to know every concept before actually answering the illustration as concepts help us a lot to reach the answer.