Question
Question: Find the value of $\cos\frac{2\pi}{13}+\cos\frac{6\pi}{13}+\cos\frac{8\pi}{13}$...
Find the value of cos132π+cos136π+cos138π
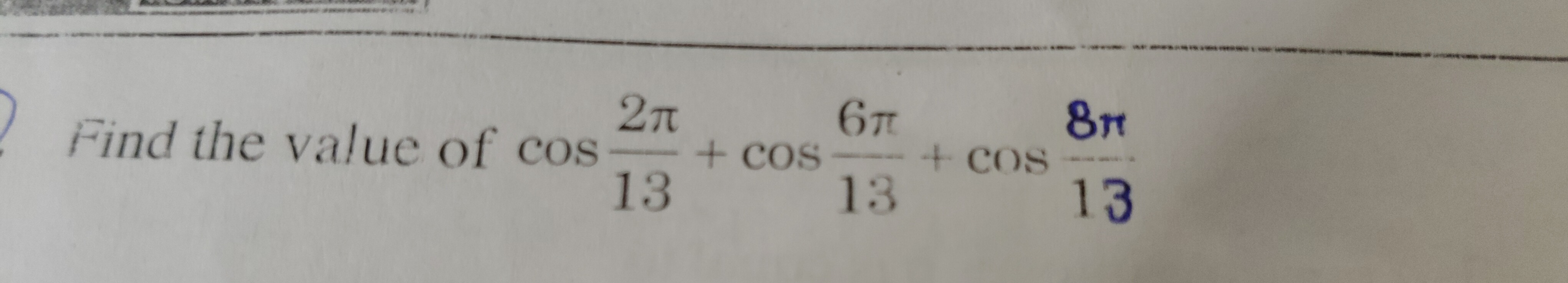
413−1
413−1
Solution
The problem asks for the value of the sum cos132π+cos136π+cos138π.
Let θ=132π. The sum can be written as S=cosθ+cos3θ+cos4θ.
We know that for a prime n, the sum of the n-th roots of unity is zero. 1+ein2π+ein4π+⋯+ein2(n−1)π=0. Taking the real part, we get: 1+cosn2π+cosn4π+⋯+cosn2(n−1)π=0. For n=13: 1+∑k=112cos132kπ=0. So, ∑k=112cos132kπ=−1.
Notice the symmetry property of cosine: cos(2π−x)=cosx. cos132kπ=cos(2π−132kπ)=cos(13(26−2k)π)=cos(132(13−k)π). This means: cos132π=cos1324π cos134π=cos1322π cos136π=cos1320π cos138π=cos1318π cos1310π=cos1316π cos1312π=cos1314π
Using this symmetry, we can rewrite the sum ∑k=112cos132kπ: 2(cos132π+cos134π+cos136π+cos138π+cos1310π+cos1312π)=−1. Let C=cos132π+cos134π+cos136π+cos138π+cos1310π+cos1312π. So, C=−21.
Let the given sum be S1=cos132π+cos136π+cos138π. Let the remaining terms in C be S2=cos134π+cos1310π+cos1312π. Then S1+S2=C=−21.
Now, let's analyze S1 and S2 using the property cos(π−x)=−cosx: S1=cos132π+cos136π+cos138π. Notice that 138π=π−135π, so cos138π=−cos135π. S1=cos132π+cos136π−cos135π.
For S2: cos1310π=cos(π−133π)=−cos133π. cos1312π=cos(π−13π)=−cos13π. So, S2=cos134π−cos133π−cos13π.
This looks like a problem related to Gaussian periods. For a prime p, the sum of cosines of angles 2kπ/p where k are quadratic residues or non-residues modulo p can be evaluated. For p=13: Quadratic residues modulo 13 are Q={12,22,32,42,52,62}(mod13)={1,4,9,3,12,10}. In increasing order: Q={1,3,4,9,10,12}. Quadratic non-residues modulo 13 are N={2,5,6,7,8,11}.
Consider the sum η0=∑k∈Qei2kπ/13. Its real part is Re(η0)=∑k∈Qcos(2kπ/13). Re(η0)=cos132π+cos136π+cos138π+cos1318π+cos1320π+cos1324π. Using symmetry cos132kπ=cos132(13−k)π: cos1318π=cos132(13−9)π=cos138π. cos1320π=cos132(13−10)π=cos136π. cos1324π=cos132(13−12)π=cos132π. So, Re(η0)=2(cos132π+cos136π+cos138π)=2S1.
Consider the sum η1=∑k∈Nei2kπ/13. Its real part is Re(η1)=∑k∈Ncos(2kπ/13). Re(η1)=cos134π+cos1310π+cos1312π+cos1314π+cos1316π+cos1322π. Using symmetry: cos1314π=cos1312π. cos1316π=cos1310π. cos1322π=cos134π. So, Re(η1)=2(cos134π+cos1310π+cos1312π)=2S2.
We know that 1+∑k=112cos132kπ=0, which implies 1+Re(η0)+Re(η1)=0. So, 1+2S1+2S2=0, which means 2(S1+S2)=−1, or S1+S2=−1/2. This matches our earlier result.
For a prime p≡1(mod4), the Gaussian periods are given by: 2Re(η0)=−1+p 2Re(η1)=−1−p Since 13≡1(mod4), we can use these formulas. We are looking for S1. We found that 2S1=Re(η0). So, 2S1=2−1+13. Therefore, S1=4−1+13.
The final answer is 413−1.
Explanation of the solution:
- Utilize Sum of Roots of Unity: The sum of the n-th roots of unity is zero. For z13−1=0, the roots are ei132kπ for k=0,1,…,12. The sum of these roots is zero. Taking the real part, we get 1+∑k=112cos132kπ=0, which implies ∑k=112cos132kπ=−1.
- Exploit Cosine Symmetry: Use the property cos(2π−x)=cosx to show that cos132kπ=cos132(13−k)π. This means the terms in the sum repeat, allowing us to write 2(cos132π+cos134π+cos136π+cos138π+cos1310π+cos1312π)=−1. Let CP=cos132π+cos134π+cos136π+cos138π+cos1310π+cos1312π. So CP=−1/2.
- Connect to Gaussian Periods: The given sum cos132π+cos136π+cos138π corresponds to the terms whose indices k are quadratic residues modulo 13 (i.e., 1,3,4). The quadratic residues modulo 13 are Q={1,3,4,9,10,12}. The sum of cosines for these indices is ∑k∈Qcos132kπ=cos132π+cos136π+cos138π+cos1318π+cos1320π+cos1324π. Using symmetry again, this sum is 2(cos132π+cos136π+cos138π), which is 2S1. This sum is the real part of the Gaussian period η0=∑k∈Qei2kπ/13.
- Apply Formula for Gaussian Periods: For a prime p≡1(mod4), the real part of the Gaussian period η0 is given by Re(η0)=2−1+p. Since 13≡1(mod4), we have Re(η0)=2−1+13. As 2S1=Re(η0), we have 2S1=2−1+13. Therefore, S1=4−1+13.
Answer:
The value of cos132π+cos136π+cos138π is 413−1.
