Question

Find the value of $\cos \left( {\dfrac {\pi }{{15}}} \right)\cos \left( {\dfrac {{2\pi }}{{15}}} \right)\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{4\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)\cos \left( {\dfrac {{7\pi }}{{15}}} \right)$

Answer 1

Here we use the formula of $2\sin x\cos x = \sin 2x$ repeatedly to lessen the values in the solution. We multiply and divide the given value with $2\sin \dfrac {\pi }{{15}}$ and apply the trigonometric formula. We continue in this manner till we stop getting the corresponding cosine of the angle in the available terms. Then break the remaining angles in terms of subtraction or addition to $\pi$ and use the quadrant diagram to solve for the value.

• In a quadrant diagram we have trigonometric functions specific to a quadrant where they are positive in nature. We always move in an anticlockwise direction when adding angles.
  

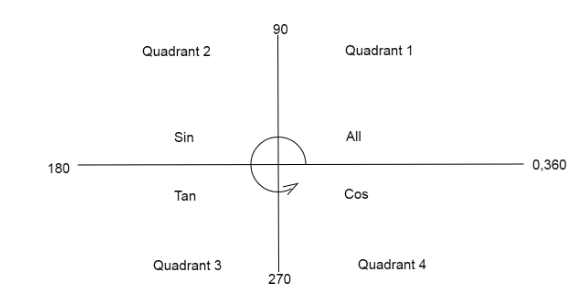
Complete step-by-step answer:
We are given the equation $\cos \left( {\dfrac {\pi }{{15}}} \right)\cos \left( {\dfrac {{2\pi }}{{15}}} \right)\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{4\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)\cos \left( {\dfrac {{7\pi }}{{15}}} \right)$
First multiply and divide the equation by $2\sin \left( {\dfrac {\pi }{{15}}} \right)$
\Rightarrow \dfrac {{\left\\{ {2\sin \left( {\dfrac {\pi }{{15}}} \right)\cos \left( {\dfrac {\pi }{{15}}} \right)} \right\\}\cos \left( {\dfrac {{2\pi }}{{15}}} \right)\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{4\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)\cos \left( {\dfrac {{7\pi }}{{15}}} \right)}}{{2\sin \left( {\dfrac {\pi }{{15}}} \right)}}
Use the trigonometric formula $2\sin x\cos x = \sin 2x$. Substitute $x = \dfrac {\pi }{{15}}$
$2\sin \dfrac {\pi }{{15}}\cos \dfrac {\pi }{{15}} = \sin 2\dfrac {\pi }{{15}}$
Multiply the value in RHS
$2\sin \dfrac {\pi }{{15}}\cos \dfrac {\pi }{{15}} = \sin \dfrac {{2\pi }}{{15}}$ … (2)
Substitute the value from equation (2) in equation (1)
$\Rightarrow \dfrac {{\sin \left( {\dfrac {{2\pi }}{{15}}} \right)\cos \left( {\dfrac {{2\pi }}{{15}}} \right)\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{4\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)\cos \left( {\dfrac {{7\pi }}{{15}}} \right)}}{{2\sin \left( {\dfrac {\pi }{{15}}} \right)}}$
Multiply and divide the equation by 2
\Rightarrow \dfrac {{\left\\{ {2\sin \left( {\dfrac {{2\pi }}{{15}}} \right)\cos \left( {\dfrac {{2\pi }}{{15}}} \right)} \right\\}\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{4\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)\cos \left( {\dfrac {{7\pi }}{{15}}} \right)}}{{2 \times 2\sin \left( {\dfrac {\pi }{{15}}} \right)}} … (3)
Use the trigonometric formula$2\sin x\cos x = \sin 2x$. Substitute $x = \dfrac {{2\pi }}{{15}}$
$2\sin \dfrac {{2\pi }}{{15}}\cos \dfrac {{2\pi }}{{15}} = \sin 2\dfrac {{2\pi }}{{15}}$
Multiply the value in RHS
$2\sin \dfrac {{2\pi }}{{15}}\cos \dfrac {{2\pi }}{{15}} = \sin \dfrac {{4\pi }}{{15}}$ … (4)
Substitute the value from equation (4) in equation (3)
$\Rightarrow \dfrac {{\sin \left( {\dfrac {{4\pi }}{{15}}} \right)\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{4\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)\cos \left( {\dfrac {{7\pi }}{{15}}} \right)}}{{4\sin \left( {\dfrac {\pi }{{15}}} \right)}}$
Multiply and divide the equation by 2
\Rightarrow \dfrac {{\left\\{ {2\sin \left( {\dfrac {{4\pi }}{{15}}} \right)\cos \left( {\dfrac {{4\pi }}{{15}}} \right)} \right\\}\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)\cos \left( {\dfrac {{7\pi }}{{15}}} \right)}}{{2 \times 4\sin \left( {\dfrac {\pi }{{15}}} \right)}} … (5)
Use the trigonometric formula$2\sin x\cos x = \sin 2x$. Substitute $x = \dfrac {{4\pi }}{{15}}$
$2\sin \dfrac {{4\pi }}{{15}}\cos \dfrac {{4\pi }}{{15}} = \sin 2\dfrac {{4\pi }}{{15}}$
Multiply the value in RHS
$2\sin \dfrac {{4\pi }}{{15}}\cos \dfrac {{4\pi }}{{15}} = \sin \dfrac {{8\pi }}{{15}}$ … (6)
Substitute the value from equation (6) in equation (5)
$\Rightarrow \dfrac {{\sin \left( {\dfrac {{8\pi }}{{15}}} \right)\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)\cos \left( {\dfrac {{7\pi }}{{15}}} \right)}}{{8\sin \left( {\dfrac {\pi }{{15}}} \right)}}$ … (7)
Now we know $\cos \left( {\dfrac {{7\pi }}{{15}}} \right) = \cos \left( {\pi - \dfrac {{8\pi }}{{15}}} \right)$
We find the value of $\cos \left( {\dfrac {{7\pi }}{{15}}} \right)$ from the quadrant diagram.

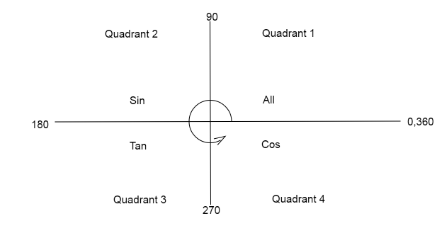
As we subtract an angle from $\pi$, only the function sin remains positive.
Therefore, $\cos \left( {\pi - \dfrac {{8\pi }}{{15}}} \right) = - \cos \left( {\dfrac {{8\pi }}{{15}}} \right)$
Substitute the value of $\cos \left( {\dfrac {{7\pi }}{{15}}} \right) = - \cos \left( {\dfrac {{8\pi }}{{15}}} \right)$ in equation (7)
$\Rightarrow \dfrac {{ - \sin \left( {\dfrac {{8\pi }}{{15}}} \right)\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)\cos \left( {\dfrac {{8\pi }}{{15}}} \right)}}{{8\sin \left( {\dfrac {\pi }{{15}}} \right)}}$
Multiply and divide the equation by 2
\Rightarrow \dfrac {{ - \left\\{ {2\sin \left( {\dfrac {{8\pi }}{{15}}} \right)\cos \left( {\dfrac {{8\pi }}{{15}}} \right)} \right\\}\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)}}{{2 \times 8\sin \left( {\dfrac {\pi }{{15}}} \right)}} … (8)
Use the trigonometric formula$2\sin x\cos x = \sin 2x$. Substitute $x = \dfrac {{8\pi }}{{15}}$
$2\sin \dfrac {{8\pi }}{{15}}\cos \dfrac {{8\pi }}{{15}} = \sin 2\dfrac {{8\pi }}{{15}}$
Multiply the value in RHS
$2\sin \dfrac {{8\pi }}{{15}}\cos \dfrac {{8\pi }}{{15}} = \sin \dfrac {{16\pi }}{{15}}$ … (9)
Substitute the value from equation (9) in equation (8)
$\Rightarrow \dfrac {{ - \sin \left( {\dfrac {{16\pi }}{{15}}} \right)\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)}}{{16\sin \left( {\dfrac {\pi }{{15}}} \right)}}$ … (10)
Now we know $\sin \left( {\dfrac {{16\pi }}{{15}}} \right) = \sin \left( {\pi + \dfrac {\pi }{{15}}} \right)$
We find the value of $\sin \left( {\dfrac {{16\pi }}{{15}}} \right)$ from the quadrant diagram.

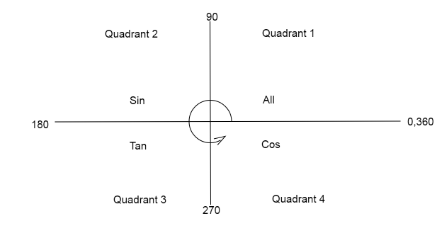
As we add an angle to $\pi$, only the function tan remains positive.
Therefore, $\sin \left( {\pi + \dfrac {\pi }{{15}}} \right) = - \sin \left( {\dfrac {\pi }{{15}}} \right)$
Substitute the value of $\sin \left( {\dfrac {{16\pi }}{{15}}} \right) = - \sin \left( {\dfrac {\pi }{{15}}} \right)$ in equation (10)
$\Rightarrow \dfrac {{ - ( - \sin \left( {\dfrac {\pi }{{15}}} \right))\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)}}{{16\sin \left( {\dfrac {\pi }{{15}}} \right)}}$
Cancel the same terms from numerator and denominator.
$\Rightarrow \dfrac {{\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)}}{{16}}$
$\Rightarrow \dfrac {{\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {\pi }{3}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)}}{{16}}$
Substitute the value of $\cos \left( {\dfrac {\pi }{3}} \right) = \dfrac {1}{2}$
$\Rightarrow \dfrac {{\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)}}{{16 \times 2}}$
$\Rightarrow \dfrac {{\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)}}{{32}}$ … (11)
First multiply and divide the equation by $2\sin \left( {\dfrac {{3\pi }}{{15}}} \right)$
\Rightarrow \dfrac {{\left\\{ {2\sin \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{3\pi }}{{15}}} \right)} \right\\}\cos \left( {\dfrac {{6\pi }}{{15}}} \right)}}{{32 \times 2\sin \left( {\dfrac {{3\pi }}{{15}}} \right)}} … (12)
Use the trigonometric formula $2\sin x\cos x = \sin 2x$. Substitute $x = \dfrac {{3\pi }}{{15}}$
$2\sin \dfrac {{3\pi }}{{15}}\cos \dfrac {{3\pi }}{{15}} = \sin 2\dfrac {{3\pi }}{{15}}$
Multiply the value in RHS
$2\sin \dfrac {{3\pi }}{{15}}\cos \dfrac {{3\pi }}{{15}} = \sin \dfrac {{6\pi }}{{15}}$ … (13)
Substitute the value from equation (13) in equation (12)
$\Rightarrow \dfrac {{\sin \left( {\dfrac {{6\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)}}{{64\sin \left( {\dfrac {{3\pi }}{{15}}} \right)}}$
Multiply and divide the equation by 2
\Rightarrow \dfrac {{\left\\{ {2\sin \left( {\dfrac {{6\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)} \right\\}}}{{2 \times 64\sin \left( {\dfrac {{3\pi }}{{15}}} \right)}} … (14)
Use the trigonometric formula $2\sin x\cos x = \sin 2x$. Substitute $x = \dfrac {{6\pi }}{{15}}$
$2\sin \dfrac {{6\pi }}{{15}}\cos \dfrac {{6\pi }}{{15}} = \sin 2\dfrac {{6\pi }}{{15}}$
Multiply the value in RHS
$2\sin \dfrac {{6\pi }}{{15}}\cos \dfrac {{6\pi }}{{15}} = \sin \dfrac {{12\pi }}{{15}}$ … (15)
Substitute the value from equation (15) in equation (14)
$\Rightarrow \dfrac {{\sin \left( {\dfrac {{12\pi }}{{15}}} \right)}}{{128\sin \left( {\dfrac {{3\pi }}{{15}}} \right)}}$ … (16)
Now we know $\sin \left( {\dfrac {{12\pi }}{{15}}} \right) = \sin \left( {\pi - \dfrac {{3\pi }}{{15}}} \right)$
We find the value of $\sin \left( {\dfrac {{12\pi }}{{15}}} \right)$from the quadrant diagram.

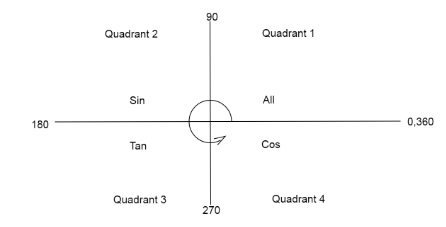
As we subtract an angle from$\pi$, only the function sin remains positive.
Therefore, $\sin \left( {\pi - \dfrac {{3\pi }}{{15}}} \right) = \sin \left( {\dfrac {{3\pi }}{{15}}} \right)$
Substitute the value of $\sin \left( {\dfrac {{12\pi }}{{15}}} \right) = \sin \left( {\dfrac {{3\pi }}{{15}}} \right)$ in equation (16)
$\Rightarrow \dfrac {{\sin \left( {\dfrac {{3\pi }}{{15}}} \right)}}{{128\sin \left( {\dfrac {{3\pi }}{{15}}} \right)}}$
Cancel the same terms from numerator and denominator.
$\Rightarrow \dfrac {1}{{128}}$
Therefore, value of $\cos \left( {\dfrac {\pi }{{15}}} \right)\cos \left( {\dfrac {{2\pi }}{{15}}} \right)\cos \left( {\dfrac {{3\pi }}{{15}}} \right)\cos \left( {\dfrac {{4\pi }}{{15}}} \right)\cos \left( {\dfrac {{5\pi }}{{15}}} \right)\cos \left( {\dfrac {{6\pi }}{{15}}} \right)\cos \left( {\dfrac {{7\pi }}{{15}}} \right)$ is$\dfrac {1}{{128}}$.

Note: Students are likely to get confused while pairing up the values for cos and sin after the value of angle as $\dfrac {{8\pi }}{{15}}$, keep in mind we break the angle with addition and subtraction to $\pi$. Always check the angle from the quadrant diagram as when we add an angle we move in anticlockwise direction and when we subtract an angle we move in clockwise direction.