Question

Find the value of $\cos 1{}^\circ \cos 2{}^\circ \cos 3{}^\circ ..........\cos 180{}^\circ$.

Answer 1

Hint: We will try to trace the value of $\cos \theta$ in the first quadrant and second quadrant using its graph. And finally multiply all the values to get the result. We will also check whether any value $\theta$ of $\cos \theta$ is $0$ and if it is then it will change all the values because all the values are in multiplication with each other anything multiplied by zero is zero.

Complete step by step answer:

It is given in the question that to find the value of $\cos 1{}^\circ \cos 2{}^\circ \cos 3{}^\circ ..........\cos 180{}^\circ$. All the values of $\cos \theta$ are in multiplication with each other. Now, we will check the nature of $\cos \theta$ in the first quadrant and second quadrant.

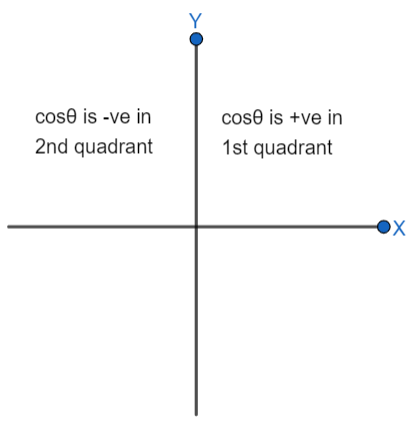
$\begin{aligned} & \cos 1=+cos(179) \\\ & cos2=+cos(178) \\\ & cos3=+cos(177) \\\ \end{aligned}$
And so on
But we will look at the value of $\cos 90{}^\circ$ that is $0$. As, the value of $\cos 90{}^\circ$ is zero. When the value of $\cos 90{}^\circ$ is multiplied by any term it will become zero.
Therefore, the whole equation will be zero.

Note: Students may not solve these types of questions in example because most of them think that it is very long and time consuming but, if we understand what actually the question has demanded. Then, it can be solved even orally. The question is not lengthy but tricky. So, use your own intelligence to solve such questions.