Question

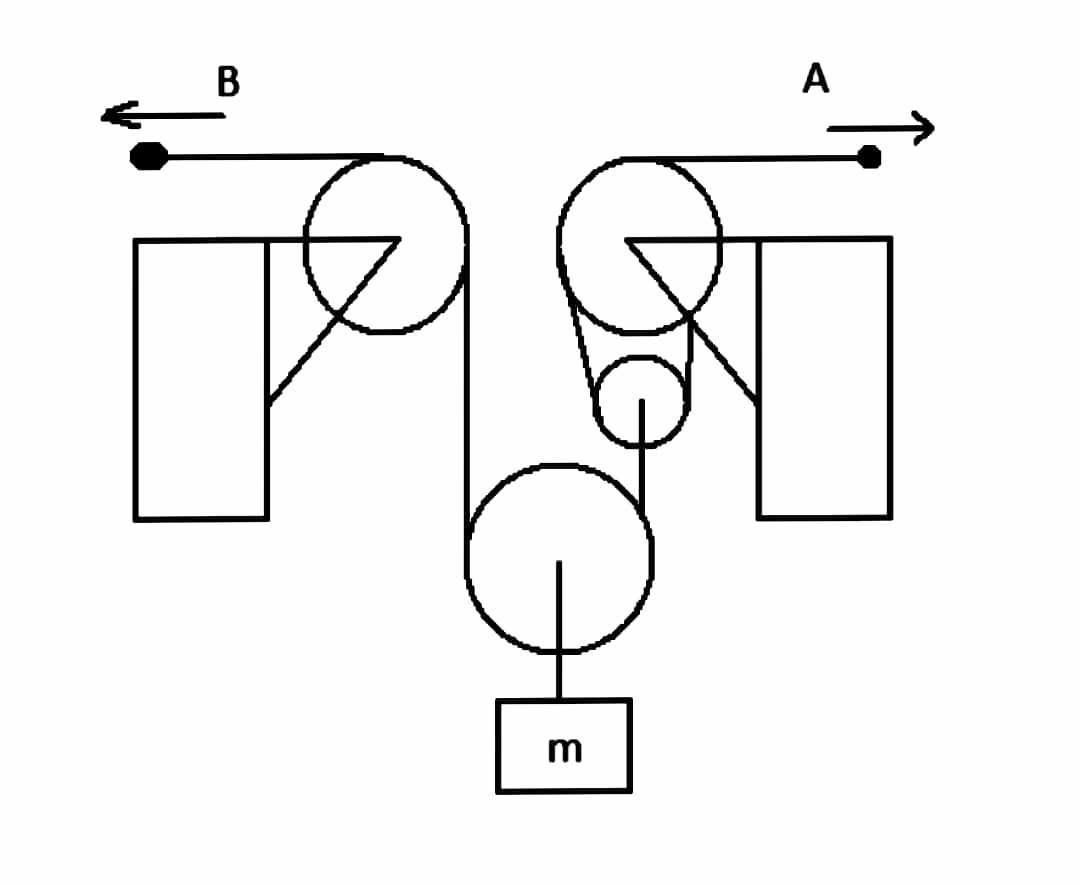
Find the upward velocity $V$ of load $m$ in the pulley system as shown in figure in which each cable at $A$ and $B$ is given velocity of $2m/\sec$ in the direction of the arrow.

(A) $1.5m/\sec$
(B) $3m/\sec$
(C) $6.3m/\sec$
(D) $4.5m/\sec$

Answer 1

Use the relation of constraint motion for pulley to find the expression for upward velocity $V$ of pulley and use the given velocity of cables in the expression of upward velocity.

Complete Step by Step Solution: -
According to the question, it is given that –
Let the velocity of each cables $A$ and $B$ be $v$ and let the upward velocity of mass $m$ be $V$
Therefore, velocity of each cable $A$ and $B$, $v = 2m/\sec$
For getting the answer the figure given in question can be drawn as –

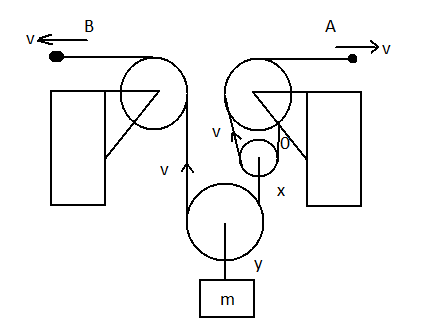
Now, from the figure using the constraint relation of pulley, we get –
$x = \dfrac{{v + 0}}{2} \\\ \Rightarrow x = \dfrac{v}{2} \cdots \left( 1 \right) \\\$
Now, the value of $y$ from the figure can be given by –
$y = \dfrac{{v + x}}{2} \cdots \left( 2 \right)$
Using the value of $x$ from equation $\left( 1 \right)$ in equation $\left( 2 \right)$, we get –
$y = \dfrac{{v + \dfrac{v}{2}}}{2} \\\ \Rightarrow y = \dfrac{{2v + v}}{4} \\\ \Rightarrow y = \dfrac{{3v}}{4} \\\$
Now, from the figure, we can conclude that $y$ is the velocity of mass $m$. So, the upward velocity is –
$V = \dfrac{{3v}}{4}$
Putting the value of $v$ in the above equation –
$V = \dfrac{{3 \times 2}}{4} \\\ \Rightarrow V = \dfrac{6}{4} \\\ \Rightarrow V = \dfrac{3}{2}m/\sec \\\ \Rightarrow V = 1.5m/\sec \\\$
Hence, the correct option is (A).

Note: - Constraint relation states that the sum of product of all tensions is strings and velocity of respective blocks connected with the string is equal to zero. We can also say that total power by the tension is zero. This can be represented mathematically by –
$\sum {T.} \bar v = 0$
The constraint relation works only when the strings are inextensible and taut.
When it is given that specific pulley is mass less than the tensions on both the sides of that pulley are equal.