Question
Question: Find the trigonometric ratios \[\tan \theta \] and \[\cos \theta \] of an angle \[\theta \], which i...
Find the trigonometric ratios tanθ and cosθ of an angle θ, which is in standard position, whose terminal arm passes through (7,24)
Solution
First we have to know that an angle is said to be in standard position if its vertex is located at the origin and one ray is on the positive x-axis. The ray on the x-axis is called the initial side (adjacent side) and the other ray is called the terminal side (opposite side). The angle is measured by rotation from the initial side to the terminal side.
Complete answer:
First, we know that the terminal arm is in the first quadrant. The ratios tanθ and cosθ in the first quadrant are positive.
We know that tanθ=adjacentsideoppositeside and cosθ=hypotenusesideadjacentside.
At standard position given the terminal arm passes through the point (7,24)
i.e., adjacent side, x=7 and opposite side, y=24.
Let r be the hypotenuse side.
According to the Pythagoras theorem
We have r2=x2+y2
⇒r2=72+242
⇒r2=49+576
⇒r2=625
⇒r=25
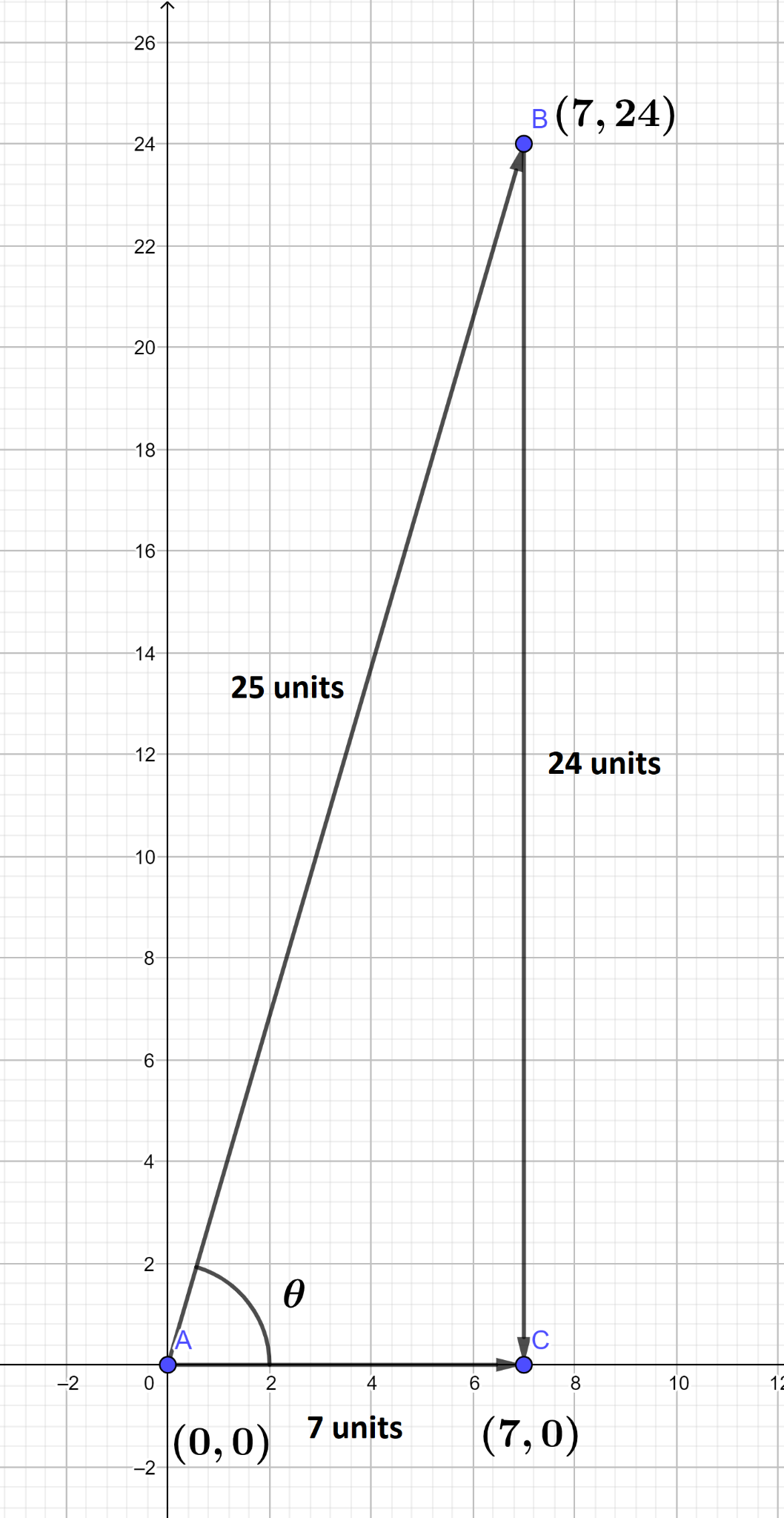
Then
tanθ=xy=724 and
cosθ=rx=257.
Note:
Note that the six basic trigonometric ratios are sine, cosine, tangent, cosecant, secant, and cotangent. All these trigonometric ratios are defined using the sides of the right triangle, such as an adjacent side, opposite side, and hypotenuse side. Also, the standard angles for these trigonometric ratios are 0o, 30o, 45o, 60o and 90o.
