Question
Question: Find the tension in the string connecting the blocks if \(F\text{ is 100N}\). \(\begin{aligned} ...
Find the tension in the string connecting the blocks if F is 100N.
A. 25NB. 46NC. 32ND. 18N
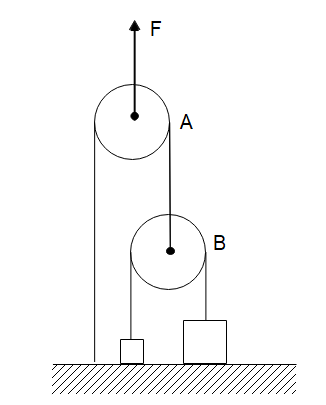
Solution
This type of question can be solved by defining tension in each string. The tension is a type of force that acts along the length of the body. Form an equation in which the tension in the string is balanced by other resultant forces for both the pulleys separately and calculate the value of the tension.
Complete step-by-step answer:
We have given a diagram in which two pulleys A and B are used. Upper pulley (A) has two strings, one is connected to ground where the second string is attached to the lower pulley. Lower pulley has carried two boxes. Also, we can see that the weight is attached to each of the strings because of which tension is produced in the string.
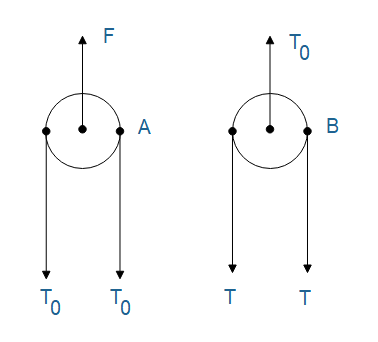
Let’s talk about first pulley A:
Because of the ground and pulley B, the tension produced in both the strings isT0.
These two tensions T0and T0 are balanced by the forceF.
Mathematically,
2T0=F
Talking about pulley B:
Because two boxes are attached to the strings, tension is produced in both the strings.
These two tensions, T and T are balanced by the tension T0 as shown in the figure.
Mathematically,
2T=T0
Now, put the value of T0 in the first equation, we get
2(2T)=1004T=100T=25N
Therefore, the tension in the string connecting the blocks is 25N.
Note: We know that the SI unit of the tension is Newton, denoted byN. The tension is one of the types of force that is produced when mass is attached to a string under gravitational force. Therefore, the unit of tension and force are the same. The CGS unit of the tension is dyne. Students usually get confused between the stress and the tension. Remember that, tension is the force acting along the length when an object is pulled from both sides whereas stress is the effect of force acting on an object.
