Question

Find the tension in the string A just after the string B is cut.

Answer 1

We have been given a rod which is connected to two strings. Once the string is cut off the rod accelerates towards A due to the absence of the balancing tension at B. The tension in the string A, immediately after B is cut off will be given Newton’s second law, as the rod is accelerating w.r.t the center of mass. The acceleration can be found by analyzing the torque acting about point A.
Formula used:
\eqalign{ & \tau = Tl \cr & \tau = I\alpha \cr & \alpha = \dfrac{a}{l} \cr}

Complete answer:
Let’s say that the mass of the rod is $m$ and the length is $l$. The tension, say, T in the strings before cutting will have x and y components, which can be understood from the free body diagram.

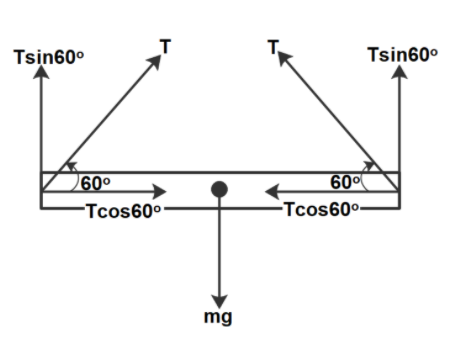
The horizontal components will cancel each other as they are equal and opposite. The vertical components will balance the weight of the rod, which can be written as
\eqalign{ & 2T\sin 60^\circ = mg \cr & \Rightarrow 2T \times \dfrac{{\sqrt 3 }}{2} = mg \cr & \Rightarrow T = \dfrac{{mg}}{{\sqrt 3 }} \cr}
Thus, the tension in the string before cutting is $T = \dfrac{{mg}}{{\sqrt 3 }}$.
Once the string B is cut off the rod accelerates towards A. The rod exerts a force of, equal to its tension, as the tension at B is absent to balance it. This force acts at a length of $l$ from point A. As one end is fixed, the torque experienced at point A will be
\eqalign{ & \tau = T\sin 60^\circ l \cr & \Rightarrow \tau = \dfrac{{mg}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{2} \times l \cr & \Rightarrow \tau = \dfrac{{mgl}}{2} - - - > eq.1 \cr}
The torque, say τ acting at B is given by
$\tau = I\alpha$
Where,
I is the moment of inertia w.r.t A, as the body is rotating about A; and
α is the angular acceleration.
The moment of inertia of a rod about one of its ends is given by $I = \dfrac{1}{3}m{l^2}$.
Substituting these in the formula for torque we have
\eqalign{ & \tau = I\alpha \cr & \Rightarrow \tau = \dfrac{1}{3}m{l^2} \times \alpha \cr & \Rightarrow \tau = \dfrac{1}{3}\alpha m{l^2} - - - > eq.2 \cr}
Comparing equation 1 and 2, we get
\eqalign{ & \dfrac{1}{3}\alpha m{l^2} = \dfrac{{mgl}}{2} \cr & \Rightarrow \alpha = \dfrac{{3g}}{{2l}} \cr}
As the rod is pivoted at one end A, the torque acts at B. This torque depends an angular acceleration which is given by
$\alpha = \dfrac{a}{l}$
Where,
α is the angular acceleration;
a is the translational acceleration; and
l is the length of the rod.
The acceleration of the center of mass will be acting from half the length as it lies at the center. Its acceleration is given by
\eqalign{ & {a_{COM}} = \alpha \times \dfrac{l}{2} \cr & \Rightarrow {a_{COM}} = \dfrac{{3g}}{{2l}} \times \dfrac{l}{2} \cr & \Rightarrow {a_{COM}} = \dfrac{{3g}}{4} \cr}
When the string at B is cut off the tension in the other string at A will be, say T’. Its vertical component will act in an upward direction.

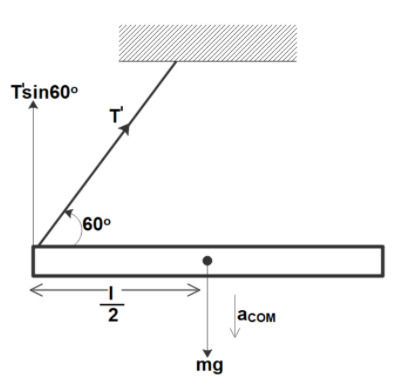
But due to weight, the rod will accelerate in a downward direction. From Newton’s second law it can be written as
\eqalign{ & m{a_{COM}} = mg - T'\sin 60^\circ \cr & \Rightarrow m \times \dfrac{{3g}}{4} = mg - T' \times \dfrac{{\sqrt 3 }}{2} \cr & \Rightarrow \dfrac{{T'}}{2} = mg - \dfrac{{3mg}}{4} \cr & \Rightarrow T' = \dfrac{{mg}}{4} \cr}
Therefore, the tension in the string A immediately after the other string is cut off is $\dfrac{{mg}}{4}$.

Note:
Tension before cutting will be the same in both the strings as the rod is having uniform mass along its length. The torque of a body is given by the vector product of force and the distance at which the force is acting from the fixed point. In the problem, the force and distance are inclined at ${60^o}$ to each other and the force acts at the other end of the rod.